Alias Method 是一种采样复杂度为 \(O(1)\) 的指定离散概率随机采样算法。一种按照给定离散概率进行随机采样方法可以简单地描述为：

给定 \(K\) 个样本，然后按照概率 \(p_{1},\dots,p_{K}\) 从中采样，那么只要将原始的 \([0,1]\) 分成 \(K\) 个区间，然后每份的长度都对应于概率的大小，然后只要从均匀分布 \(U(0,1)\) 采样，再看这个值落在哪个区间就可以实现任意分布的数据采样了。¹

看起来这个问题已经解决了，接下去就是要实现一个这样的算法：给定任意随机数，返回它应该属于哪一个区间。如果用二叉树 BST 实现数据结构的话，查询的效率在 \(O(\log N)\)，距离本文要介绍的 Alias Method 还有明显的距离。

Alisa 算法

根据 Darts, Dice, and Coins: Sampling from a Discrete Distribution² 的解释，算法整理如下：

为了解决区间查询的效率问题，Alias Method 构造了一个非常特别的数据结构。假设我们给出四个离散概率分别问 1/2、1/3、1/12、1/12。

首先对离散概率的分布做归一化，使用离散概率分布的平均概率做归一化，而不是对最大概率做归一化：

然后取四个高度为1的矩形对应到归一化后的概率分布

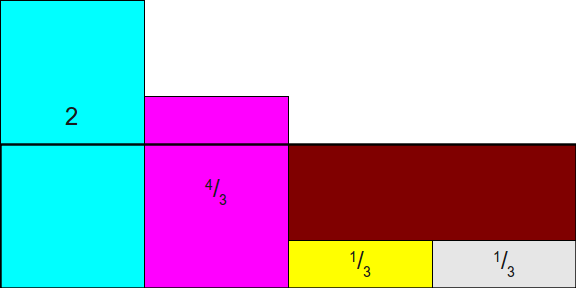
然后把高于概率1的部分分割放入到概率不满1的区块中：

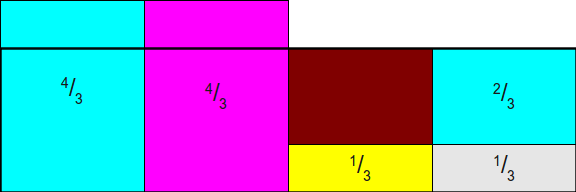
如果填满一个还没有把多出来的部分配完，那就再针对另一个没有满的区块把它填到满为止，即使让当前区块分到不足1: 在进行概率的重新划分时，需要严格遵守每个区块最多只能填入两个区块的概率值。

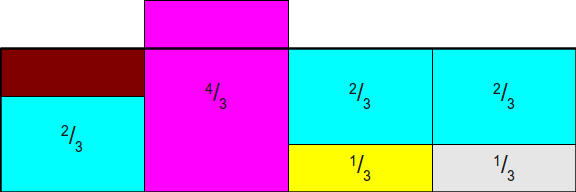
最后再取满出来的第二块去填满第一块的空缺：

最后，算法的实现方式就可以通过两个表格实现，一个用于记录原始就属于该区间的概率记作 `Prob` ，另一个存储区块编号指代第二层概率对应的区块编号记作 `Alias` 。

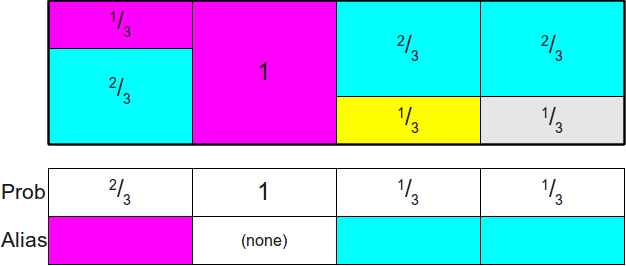
进行采样时，先随机生成一个整数值用于选择哪一列，然后再随机生成一个 0~1 之间的数字，如果大于 Prob 中的概率值，则选择使用 Alias 中的区块，否则使用原随机数。

算法实现

def alias_method_table(probs):
    K = len(probs)
		# 对应于解释中的 `Prob` 表
    S = (probs / np.sum(probs)) * K
		# 对应于解释中的 `Alias` 表
    A = np.arange(0, K)
    Tl = set(list((S < 1).nonzero()[0]))
    Th = set(list((S > 1).nonzero()[0]))

		# 不断协调两个数组直到全部安排完
    while len(Tl) > 0 and len(Th) > 0:
        j = Tl.pop()
        k = Th.pop()
        S[k] = S[k] - 1 + S[j]
        A[j] = k
        if S[k] < 1:
            Tl.add(k)
        elif S[k] > 1:
            Th.add(k)
    return S, A