变分贝叶斯的一个优势就在于它的优化对偶性。我们回顾统计推断问题（也就是通过给定其他随机变量的值来推断某一个随机变量的值）作为一个优化问题（也就是找到一批参数能够最小化某些目标函数）。更进一步的这种变分下界也称为证据下界，它时一种变分贝叶斯方法中的基本角色，我们将主要介绍这种下界的关键角色和推导。

变分贝叶斯是一类用于贝叶斯估计和机器学习领域中近似计算复杂（intractable）积分的技术。在贝叶斯推断中，参数和隐变量统称为不可观测变量（unobserved variables）。变分贝叶斯方法的主要目的有两个：

1. 近似不可观测变量的后验概率，以便通过这些变量做出统计推断
2. 对于一个特定的模型，给出观测变量的边缘似然函数（或者称为证据，evidence）的下界。主要用于模型的选择，我们认为模型的边缘似然值越高，则模型对于数据的拟合程度越好，该模型产生数据的概率也越高。

变分下界推导

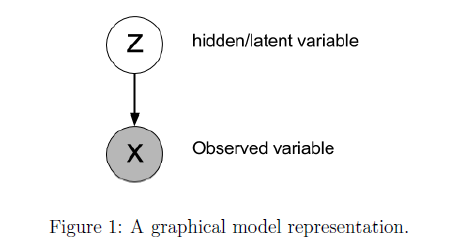
这里的 \(X\) 是我们观测到的值，这里的 \(Z\) 是隐藏的变量，通常情况下这种隐藏变量可能会有一些参数，\(X\) 和 \(Z\) 之间的关系可以用下面的这种图结构来表示。 更进一步的，大写的 \(P(X)\) 表示这个变量的概率分布，小写的这个 \(p(X)\) 表示它的概率密度函数，这个隐藏变量的后验概率分布写成贝叶斯定理也就有：

\begin{equation} P(Z|X) = \frac{p(X|Z)p(Z)}{p(X)}=\frac{p(X|Z)p(Z)}{\int_{Z}p(X,Z)} \end{equation}

Jensen 不等式

\[\begin{aligned} \log p(X) &=\log \int_{Z} p(X, Z) \\\\ &=\log \int_{Z} p(X, Z) \frac{q(Z)}{q(Z)} \\\\ &=\log \left(\mathbb{E}_{q}\left[\frac{p(X, Z)}{q(Z)}\right]\right) \\\\ & \geq \mathbb{E}_{q}\left[\log \frac{p(X, Z)}{q(Z)}\right] \\\\ &=\mathbb{E}_{q}[\log p(X, Z)]+H[Z] \end{aligned}\]

最后得到的也就是变分下界，我们也成为 ELBO。这里的\(q(Z)\)就是一个我们在变分贝叶斯中用来逼近真实的后验分布的\(p(Z\vert X)\)，在这里我们把它看成任意分布，求导仍然成立。

对于凹对数方程，可以使用 Jensen 不等式，最后一项 \(H[Z]\) 就是香侬熵 \(f(\mathbb{E}[X])\leq \mathbb{E}[f(X)]\)。那么很显然了最后得到的就是观测得到的对数似然的下界，所以，如果优化使得边缘分布概率，我们可以转而使用它的下界。

KL 散度

因为在前面的贝叶斯公式中，\(p(Z)\) 是比较难以获得的，但是它又是我们进行分布推导的动机。在很多情况下对 \(p(Z\vert X)\) 的计算是很难准确获得的，举个例子也就是我们需要把隐藏变量积分起来才能得到公式中的分母。

所以变分方法背后的主要思想也就是：找到一个近似的分布 \(q(Z)\) 并且尽可能使得它能够接近 \(p(Z\vert X)\) 的真实分布。这种近似分布可以有它们自己的变分参数：\(p(Z\vert θ)\) 我们就是需要找到一组这样的参数能够让 \(q\) 尽量地逼近我们感兴趣的那种。很显然分布 \(q(Z)\) 应该尽可能相对简单，并且更容易被用于推断。

为了衡量 \(q(Z)\) 和 \(p(Z\vert X)\) 两个分布之间的近似程度，一个常用的度量就是 KL 散度。所以用于变分推断的 KL 散度也就有：

\[\begin{aligned} K L[q(Z) \| p(Z \mid X)] &=\int_{Z} q(Z) \log \frac{q(Z)}{p(Z \mid X)} \\\\ &=-\int_{Z} q(Z) \log \frac{p(Z \mid X)}{q(Z)} \\\\ &=-\left(\int_{Z} q(Z) \log \frac{p(X, Z)}{q(Z)}-\int_{Z} q(Z) \log p(X)\right) \\\\ &=-\int_{Z} q(Z) \log \frac{p(X, Z)}{q(Z)}+\log p(X) \int_{Z} q(Z) \\\\ &=-L+\log p(X) \end{aligned}\]

其中 \(q(Z)\) 需要使用归一化的方式进行限制，也就是 \(\int_{Z}q(Z)=1\) ，重新写过最后就有：

\begin{equation} L=\log p(X)-K L[q(Z) | p(Z \mid X)] \end{equation}

例子

多目标分类

输入为图像 \(I\)，模型由参数 \(W\) 构成，其中 \(y\) 为类别标签，优化的目标就是最大化对数似然 \(\log p(y\vert I,W)\)。以上的这些随机变量都可以被认为是可观测到的。所以对于那些不能观测到的隐藏变量 \(l\)：

\begin{equation} \log p(y|I,W) = \log\sum_{l}p(l|I,W)p(y|l,I,W) \end{equation}

通过带入 Jensen 不等式可以得到它的下界就是：

\begin{equation} \log\sum_{l}p(l|I,W)p(y|l,I,W) \geq \sum_{l}p(l|I,W)\log p(y|I,W) \end{equation}

用观测所得的边缘概率分布概率的变分下界也可以得到相同的结果：

\begin{equation} \log p(y|I,W)\geq \sum_{l}q(l)\log \frac{p(y,l|I,W)}{q(l)} = \sum_{l}p(l|I,W)\log p(y|l,I,W) \end{equation}

然后就可以通过对模型参数 \(W\) 求导来最大化变分下界。