Empirical Mode Decomposition

经验模态分解（Empirical Mode Decomposition, EMD）是一种适用于非线性、非平稳信号的自适应信号分解方法。EMD方法把原始信号分解成多个固有模态函数（Intrinsic Mode Functions, IMF），EMD的提出者黄锷认为，任何信号都可以拆分成若干个固有模态函数之和，这种函数符合下面两种特征：

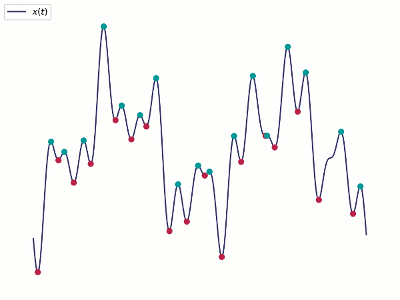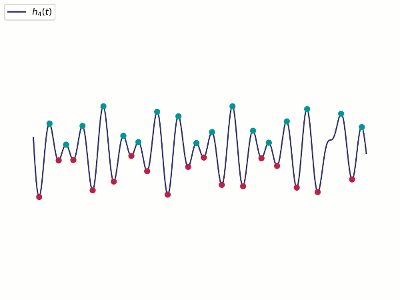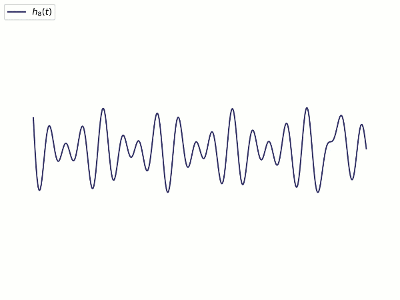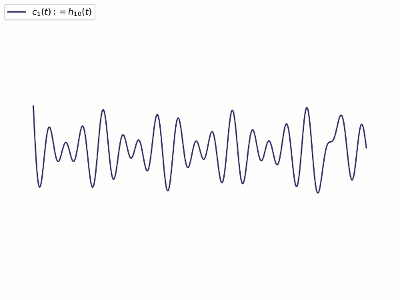
1. 在整个数据段内，极值点的个数和过零点的个数必须相等或者相差最多不超过一个。
2. 在任意时刻点，局部最大值的包络（上包络线）和局部最小值的包络（下包络线）的平均值必须为零。

希尔伯特变换

设一个实值函数\(x(t)\)，其希尔伯特变换（Hilbert Transform）记作\(\hat{x}(t)\)（或记作\(H[x(t)]\)）： \begin{equation} \hat{x}(t)=H[x(t)]=\frac{1}{\pi}\int^{\infty}_{-\infty}\frac{x(\tau)}{t-\tau}d\tau \end{equation} 对应的反变换为： \begin{equation} x(t)=H^{-1}[\hat{x}(t)]=-\frac{1}{\pi}\int^{\infty}_{-\infty}\frac{\hat{x}(\tau)}{t-\tau}d\tau \end{equation}

经验模态分解

经验模态分解是通过不断的筛选来逐步找出所有的IMF，给定一个信号\(x(t)\)，对应的筛选过程为：

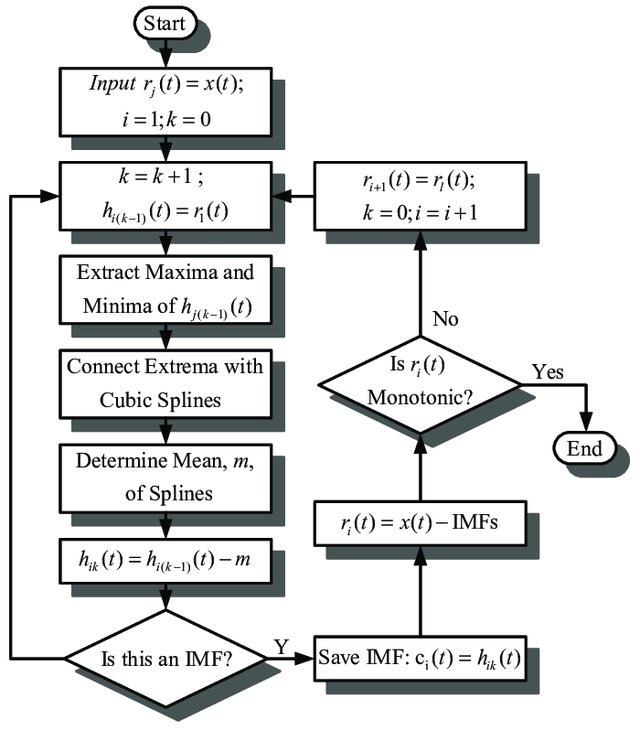
最后可以分解得到一组IMF和最后的残差分量，即n个IMF和1个单调残差分量。

停止准则

如果筛选的次数过多可能会破坏信号本身的物理性质，为了确保经验模态分析法分解出的固有模态函数能够保留顺势频率与瞬时振幅的物理意义通过设定筛选的停止准则来决定筛选的次数。

1. 标准差准则：连续两次筛选结果的分量标准差（Standard Deviation，SD）作为停止准则如下所示（一般当标准差小于0.2到0.3间时，停止筛选动作）： \begin{equation} SD=\sum^{T}_{t=0}\frac{|h_{k-1}(t)-h_{k}(t)|^{2}}{h_{k-1}(t)^{2}} \end{equation}

2. S数准则：定义过零点和极值点相等或者至多相差1的连续筛选数目。当S次连续筛选后，每一次过零点和极值点保持相同（相等或者至多差1），筛选过程才停止。

3. 能量差异追踪法：假设原始的信号\(x(t)\)包含有限个彼此不相关的正交分量\(x_{i}(t)\)： \begin{equation} x(t)=x_{1}(t)+x_{2}(t)+\dots+x_{n}(t)=\sum^{n}_{i=1}x_{i}(t) \end{equation} 原始信号\(x(t)\)的总能量可以表示为： \begin{equation} E_{x}=\int^{\infty}_{-\infty}[\sum^{n}_{i=1}x_{i}(t)]^{2}dt=\int^{\infty}_{-\infty}[\sum^{n}_{i=1}x_{i}(t)^{2}]dt \end{equation} 如果经验模态分析分解出的信号固有模态函数\(c_{1}(t)\)正好就是正交分量\(x_{1}(t)\)，则维持能量守恒，但是如果这种正交通常并不直接成立，对于分离的\(c_{1}(t)\)，它的总能量表示为： \begin{equation} E_{tot}=\int^{\infty}_{-\infty}c_{1}(t)^{2}dt+\int^{\infty}_{-\infty}[x(t)-c_{1}(t)]^{2}dt=2E_{c1}+E_{x}-2\int^{\infty}_{-\infty}x(t)c_{1}(t)dt \end{equation} 这个\(E_{tot}\neq E_{x}\)产生的一个能量差异\(E_{err}\)表示所得到的固有模态信号存在能量泄露的问题（nonorthogonal leakage），所以假设一个足够小的\(\vert E_{err}\vert\)当作停止准则，所分解出来的IMF正交性越高，信号的完整性、瞬时振幅与瞬时频率特性也会比以标准差（SD）作为停止准则要好，可以降低不必要的震荡，尤其是在初始边界的部分。

   实际在现实中，因为数据点是有限的，所以即使各个分量都是由三角曲线构成的也会引入这种正交泄露的问题。

4. 阈值准则：用两个阈值\(\theta_{1}\)和\(\theta_{2}\)作为停止准则，用上下包络线算出模态振幅\(a(t)=\frac{u_{k}(t)-l_{k}(t)}{2}\)再求出包络线均值和模态振幅的绝对比值，这个比值称为估计函数（evaluation function，\(e(t)\)）\(e(t)=\vert \frac{m(t)}{a(t)}\vert\)，当信号长度的\(1-\alpha\)部分满足\(e(t)<\theta*{1}\)，剩余的部分满足\(e(t)<\theta*{2}\)，则迭代停止。

   • \(\theta_{1}\)：确保全域的小波动为均值使得固有模态函数不会产生不必要的震荡
   • \(\theta_{2}\)：考虑到局部可能发上的间断性大偏离情况

   常见的设定值为：\(\alpha=0.05,\theta_{1}=0.05,\theta_{2}=10\theta_{1}\)。

5. 手工设定：凭借领域经验指定IMFs的数量

混模问题

混模问题是指在同一个固有模态函数里会有不同尺度的信号混杂，或者同一尺度的信号出现在不同的固有模态函数中。这种状况发生的原因是收集到的信号中有间断性信号出现，这些间断使得经验模态分解不能分解出同一个尺度的信号。而这种混模的存在也会导致分解得到的固有模态函数失去物理意义。任何扰动都可能会导致产生新的固有模态函数。所以黄锷等人提出增加噪声辅助的经验总体经验模态分解法（Ensemble Empirical Mode Decomposition），利用加入白噪声（white noise）来解决混模问题。

总体经验模态分解法

总体经验模态分解法作为一种噪声辅助的信号分析方法，首先在信号中加入白噪声（white noise），然后再对信号做经验模态分解，并重复以上步骤若干次（1000次），最后将每次分解得到对应的固有模态函数取平均来抵消噪声造成的影响。