转置卷积

反卷积（Deconvolution）很容易和信号处理中的反卷积混淆起来，其实在常见的卷积神经网络文献中应该指的是转置卷积（Transposed Convolution），下文见更准确地使用转置卷积来指代这一过程。

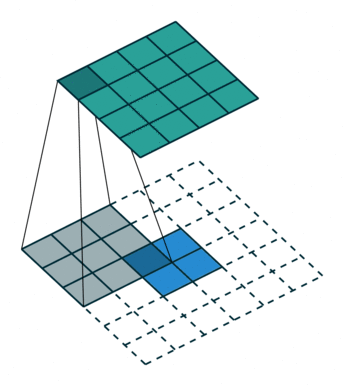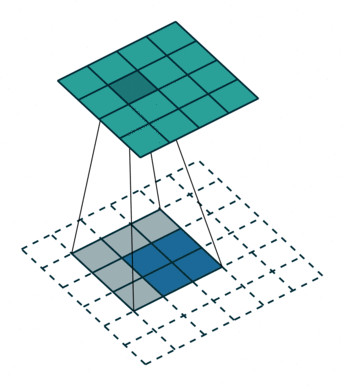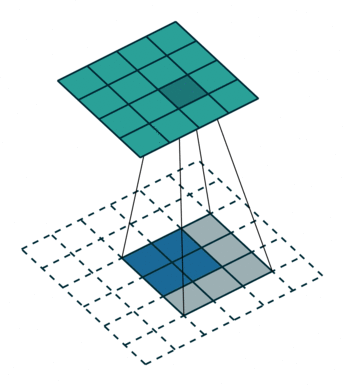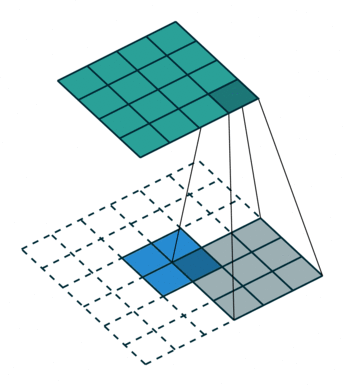
如封面示意图¹，这里的卷积都是 2 维规则方形的：

• stride：卷积核滑动步长
• padding：卷积前对原始图像进行边缘补充所用宽度的像素个数，补全方式由用户定义，一般默认补零
• kernel size：方形卷积核的边长像素个数

卷积操作

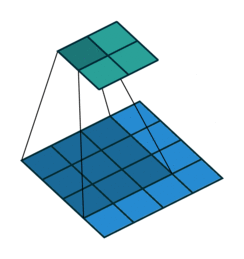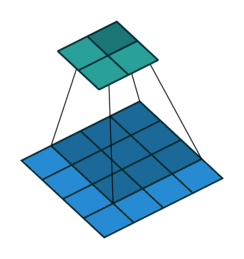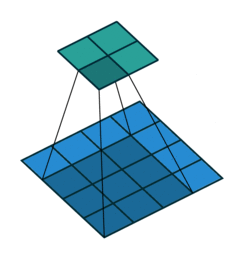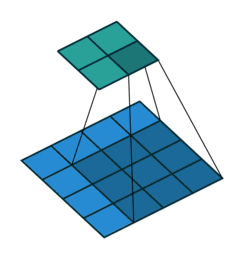
如图¹这样的卷积操作都可以写成矩阵相乘的形式：

首先看到这样的卷积操作可以通过把计算顺序写进矩阵中，然后将目标图像展平成向量，实际上在很多卷积数值实现中，都是使用这种步骤可以加速程序的执行。

通过这种重排卷积核以对应和展平成向量的图像做卷积可以得到同样展平的卷积后图像，然后对这个图像进行重排可以简单地恢复其空间结构。

转置卷积

这样转置卷积的问题就好理解了，如果要做的操作为 \(\)I{4\times 4}\otimes K{3\times 3} = C{2\times 2}\(\) 经过对卷积重排和图像展平之后就变成 \(\)K{4\times 16} \cdot I{16} = C{4}\(\) 那么要从卷积后的图像 \(C_{2\times 2}\) 得到原图像 \(I_{4\times 4}\) 就做个矩阵乘逆吧：\(\)I{16} = (K{4\times 16})^{-1} \cdot C_{4}\(\)

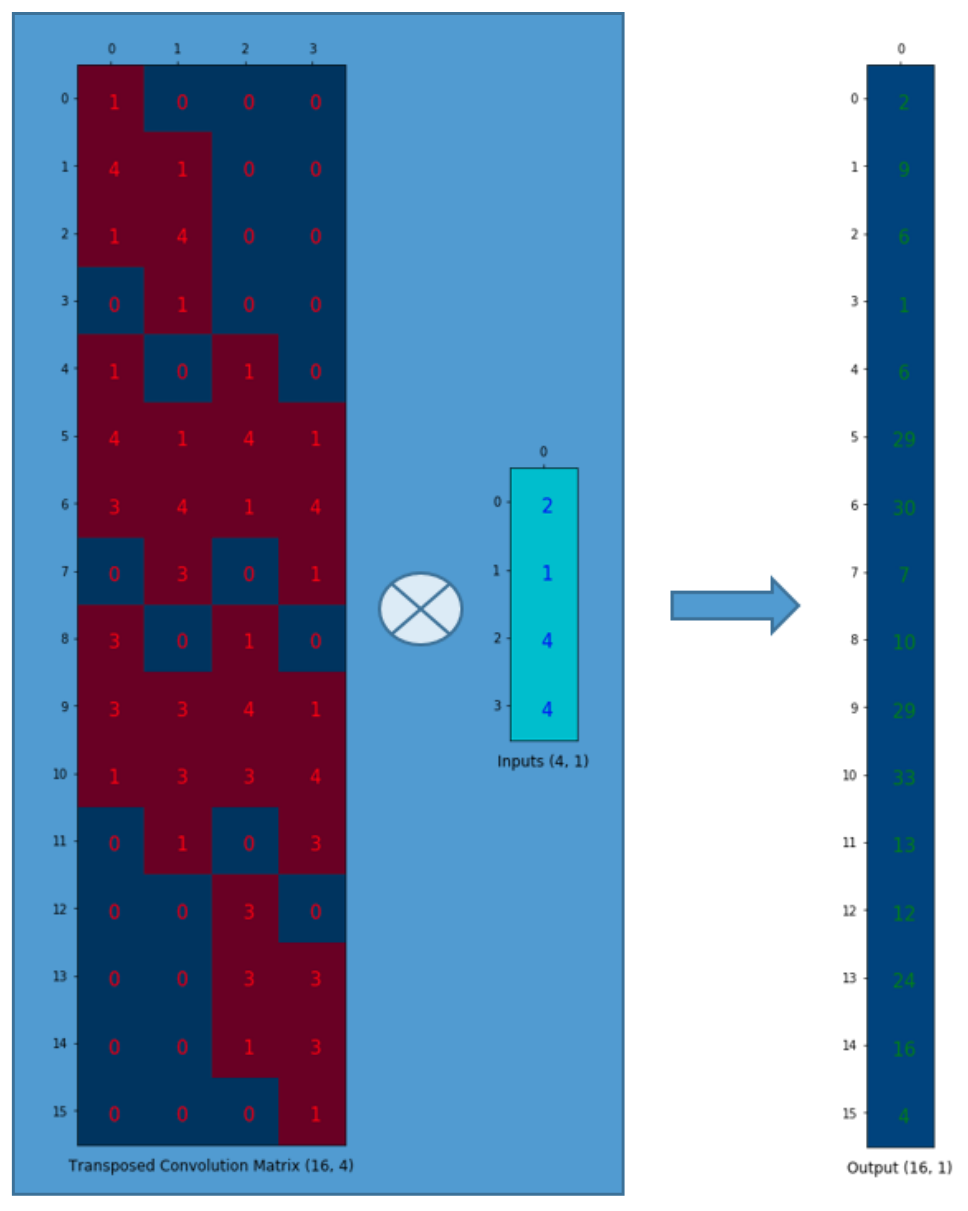
将上面的过程可视化成图像计算过程。

总结

• 卷积操作可以通过矩阵重排用更高效的方式实现
• 在矩阵实现的基础上很容易理解反卷积的规则
• 实际中不一定会严格按照这种反卷积的操作，更多的是为了保持这种卷积形状，然后通过神经网络学习得到
• 这里只说明了转置卷积的做法，在实际构建模型的时候可以有更多的操作

---