Paper | Modeling the Role of Working Memory and Episodic Memory in Behavioral Tasks

这篇文章主要研究工作记忆和情节记忆在行为任务中所承担的角色，在此之前，人们通过应用强化学习研究了很多目标导向行为的机制，但还没有明确的把记忆系统纳入到问题的考虑场景中。这篇文章从小鼠的实验文献中得到灵感，将工作记忆和情节记忆通过六个实验融入强化学习系统中，发现如果在没有延迟的任务中，只用纳入工作记忆就可以解决全部的任务，但是如果在有延迟的任务仿真中，需要工作记忆和情节记忆共同配合实现所有场景的目标完成（除了一个消除气味序列歧义的任务）。

强化学习

强化学习通过状态 \(s\) 动作 \(a\) 和奖励 \(r\) 模拟一个智能体仅仅在奖励机制的作用下如何自动学习出一套目标导向的任务。

• \(V(s)\) 表示智能体维护的状态表
• \(Q(s, a)\) 表示智能体维护的动作价值表，也就是在状态 \(s\) 下做出动作 \(a\) 的价值

这里的强化学习通过时序差分(Temporal Difference)完成，一个智能体在状态 \(s\) 做出一个动作 \(a\) 到达状态 \(s'\) 将会获得的奖励 \(r\):

\begin{equation} \delta = r+\gamma V(s’) - V(s) \end{equation}

其中 \(\gamma\) 表示时间折扣因子，如果 \(\gamma\) 越小则表示近期的回报价值更高。

\begin{equation} V(s) \leftarrow V(s)+\alpha \delta \end{equation} \begin{equation} Q(s, a) \leftarrow Q(s,a)+\alpha \delta \end{equation} 其中 \(\alpha\) 表示学习率，另外为了加速智能体的学习过程，增加一种叫做资格痕迹的东西，让当前动作带来的奖励不仅影响它刚刚离开的状态 \(s\) 估值，同时还会影响它最近访问过的那些状态估值:

\begin{equation} V(s) \leftarrow V(s) +\alpha \delta \cdot E(s, a) \end{equation} \begin{equation} Q(s,a) \leftarrow Q(s, a) + \alpha \delta \cdot E(s,a) \end{equation} 对于每一对 \(s\) 和 \(a\)，在模拟阶段 \(E(s,a)\) 会经过阈值 \(\theta\) 处理，对于当前状态和动作 \(E(s,a)\leftarrow 1\) 对于其他的状态 \(s'\) 则设置 \(E(s',a)\leftarrow \lambda E(s', a)\), 其中 \(\lambda\) 是一个延迟算子。

这样每个智能体还需要额外维护一张表 \(E(s, a)\)。

状态和动作

假设状态可以因式分解成 \(S=S_{1}\times S_{2} \times \dots \times S_{n}\)，那么状态中的元素也就是 \(n\) 分量组成的 \(\{(x_{1},x_{2}\dots,x_{n}\}\) 在这篇文章设计的实验中主要分为位置状态 \(S_{L}\) (网格中的方格数量)和工作记忆 \(S_{WM}\) 以及情节记忆 \(S_{EP}\)。

另外从生理学角度看，因为把记忆的表现和记忆的影响也作为状态信息了，也就建模了智能体脑区的多个功能区。

文中所表现的状态动作以网格的形式表现就如下图：其中黑色箭头表示正在执行的动作，灰色箭头表示其他未选择的动作，黑色方块表示不能逾越的障碍，灰色方块表示可以推动的屏障。

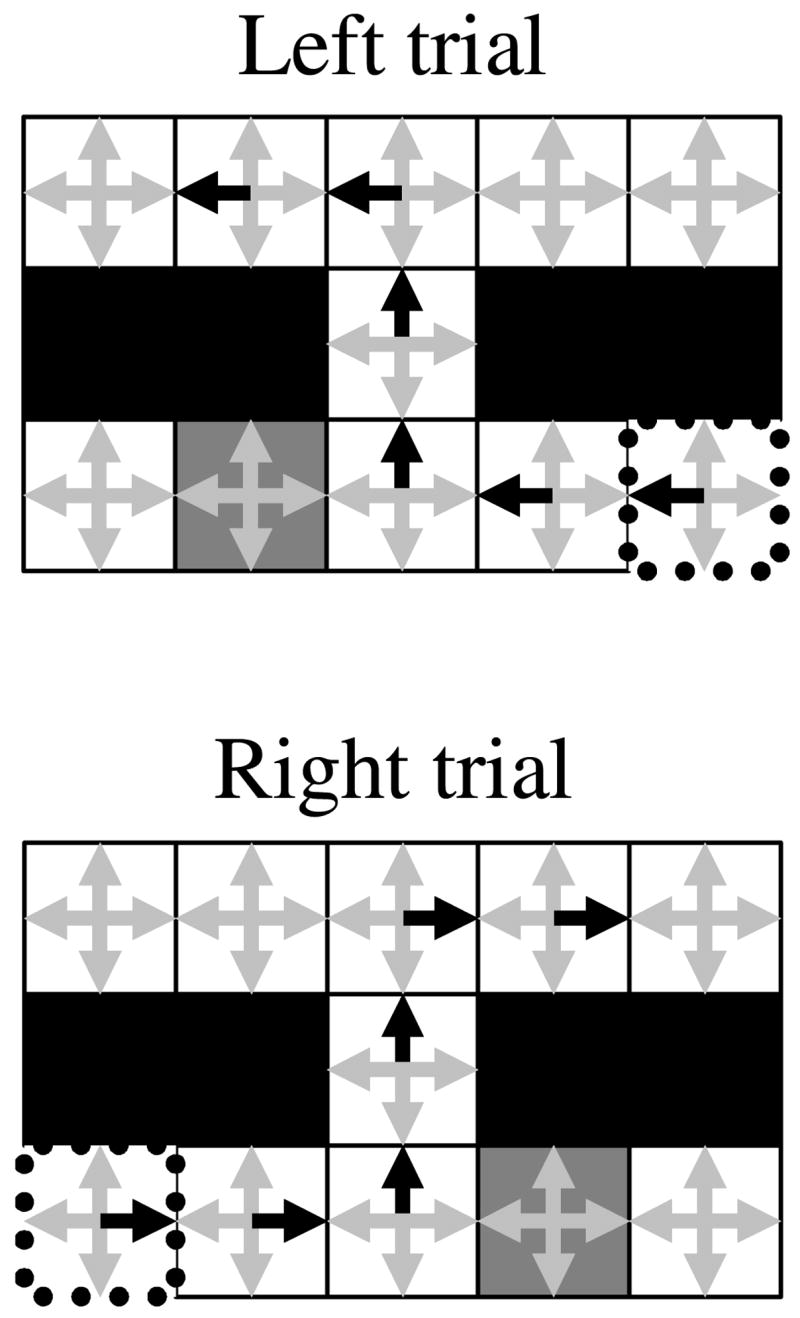
工作记忆

工作记忆有两种经典的表述方式，而两种方式的机制都是通过增加工作记忆动作的动作值学习将刺激缓冲进工作记忆的合适时间。（这听起来很绕，其实可以把这些看成一种门控模型）。这种说法和另一种模型也比较类似，考虑一组变量 \(<I,\pi, \beta>\) 其中 \(I\) 是当前状态下可用的动作集合，\(\pi\) 是一种策略，\(\beta(s)\) 给出在任意状态 \(s\) 将会终止的概率。

情节记忆

情节记忆的两个主要特征：

1. 是上下文可寻址的
2. 是按照时间索引的

第一条表示，这些记忆是可以连成线索的，也就像是能通过一个关键词牵出一整个语义场景。第二条表示，一旦回放到当时那个场景，所有在那个时刻发生的事情都可以被回忆起。

如果用 \(\mathbf{T}\) 作为一个有 \(n\) 个时间节点的二值行向量，每次只有一个元素非零，\(\mathbf{S}\) 表示所有状态存在与否的状态，是由多种状态空间串联而成的。通过一个时间提取向量，可获取记忆指标为，这种记忆形式的数学表达形式化如下，\(M\) 在每一步动作之后都会按照下面的方式更新：

\begin{equation} dM=\mathbf{T}^{T}\mathbf{S}-\mathbf{T}^{T}\mathbf{T}M \end{equation}

或者：

\begin{equation} dM = \mathbf{T}^{T}(\mathbf{S}-\mathbf{T}M) \end{equation}

其中 \(M\) 可以用突触连接权重矩阵来表示，这里的 \(dM\) 表示记忆的更新量，这样在任意一个时刻的状态都可以直接通过时间向量和记忆状态相乘获得状态，并且公式中的第一项 \(\mathbf{T}^{T}\mathbf{S}\) 表示感觉向量到时间索引向量，第二项 \(\mathbf{T}^{T}\mathbf{T}M\) 生成和 \(M\) 相同大小的矩阵：

\begin{equation} \mathbf{S}=\mathbf{T}M \end{equation}

另外又定义了为每个状态元素定义了一行的矩阵 \(N\)，其中包含了给定状态最后一次经历的时间索引向量。

\begin{equation} dN=\mathbf{S}^{T}\mathbf{T} - \sum_{i}\mathbf{S}^{T}_{i}S_{i}N \end{equation}

总结

文章通过六个实验给出了一个结论，即考虑工作记忆和情节记忆在强化学习任务中是有效的。