Paper | GLMNet: Graph Learning-Matching Networks for Feature Matching

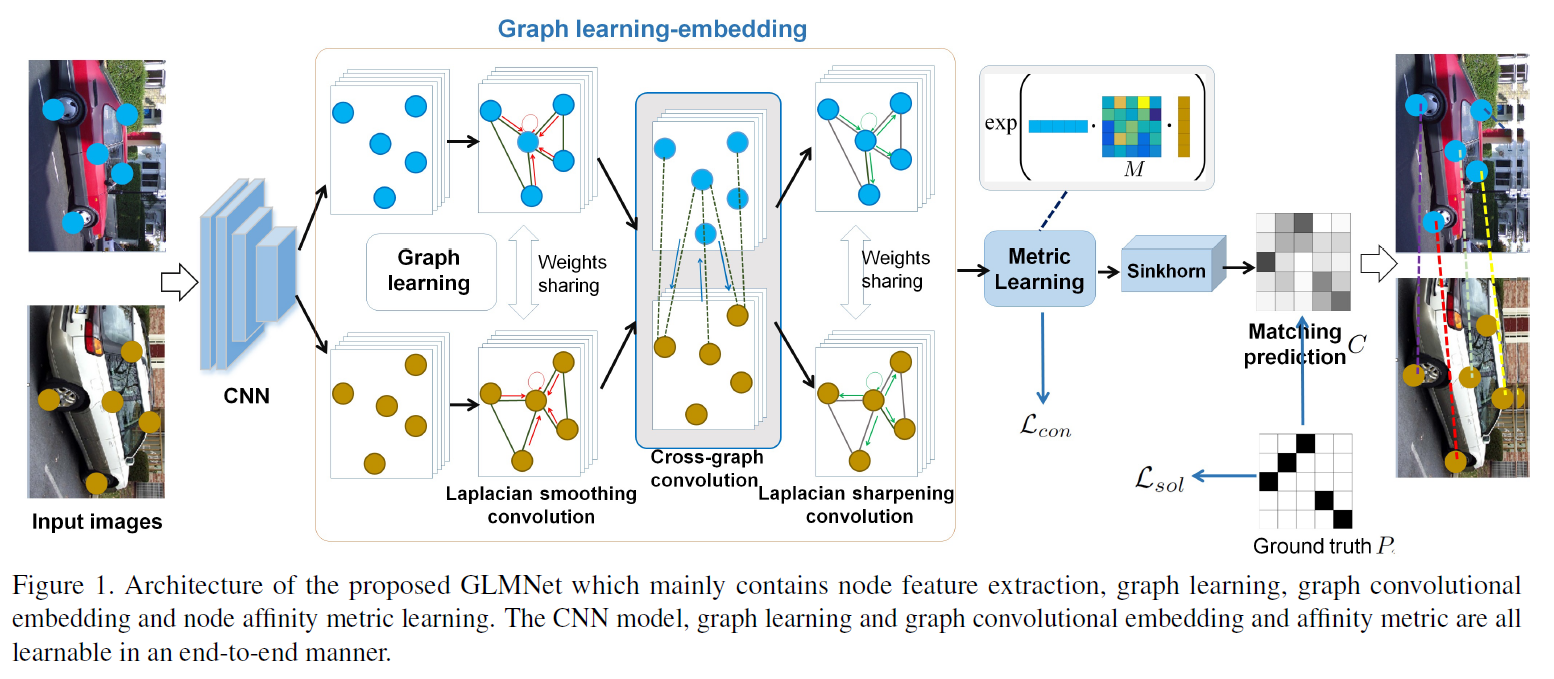
图卷积因为有较强的特征表达能力以及可以端到端的训练，在很多基于图的场景中都有比较好的表现，像是图的节点识别，图的匹配和对齐等。但是现有图匹配通常是固定的，且和图相互独立。在进行图卷积的过程中还会有加入基于平滑的卷积层，这种平滑效果会冲淡图节点的可辨识特征。所以文中提出图学习匹配网络 (GLMNet)

图匹配问题

因为图匹配涉及到图中节点和边的密切关系，这些内容编码了两个图之间的相似度，所以经常表示成二次规划问题，因为有排列组合的一对一匹配限制条件（比如一个简单的例子是二分图匹配，一个图的节点要和另一图中的节点一一对应），所以通常被看做是一个 NP 难问题。

问题形式化：用 \(\mathcal{M}\) 和 \(\mathcal{D}\) 分别表示两幅图像 \(\mathcal{I}\) 和 \(\mathcal{I}'\) 中的特征集合。目标是能将这两幅图像中的特征能够一对一地匹配上。

用 \(X=(x_{1}, x_{2}\dots x_{m})\) 和 \(Y=(y_{1},y_{2}\dots y_{n})\) 分别表示两个集合中一元特征描述子，其中 \(m\) 和 \(n\) 分别表示两个特征集合的大小。然后再用 \(A_{x},G_{y}\) 分别表示两个图中节点的二值连接关系。通过下面两个标准来衡量图匹配优度：

1. 节点描述子的匹配程度
2. 边属性的保留程度

特征提取

图中的特征可以通过在 ImageNet 上预训练过的网络提取，从 \(\mathcal{I}\) 到与之对应的内容 \(X=(x_{1}, x_{2} \dots x_{m})\in \mathbb{R}^{p\times m}\) 和 \(y=(y_{1}, y_{2} \dots y_{m})\in \mathbb{R}^{p\times n}\)，从特征提取到建图这一部分是图匹配的基础，文中采用单层神经网络来建立各个特征在图 \(G(X,A_{x})\) 中的节点关系 \(A_{x},A_{y}\) 通过基于学习的建图获得更有表达能力的图：

设 \(X=(x_{1},x_{2}\dots x_{m})\in \mathbb{R}^{n\times p}\)，神经网络需要学习到 \(A_{x}(i,j)=\phi(x_{i}, x_{j};\theta_{x})\)：

\begin{equation} A_{x}(i,j) = \phi(x_{i},x_{j};\theta_{x})=\frac{\exp (\sigma(\theta^{T}_{x}[x_{i}|x_{j}]))}{\sum^{n}_{j=1}\exp(\sigma(\theta^{T}_{x}[x_{i}|x_{j}]))} \end{equation}

其中，\(\|\) 表示串联操作，\(\sigma\) 表示激活函数，如果有初始图可用话也可以直接放入到学习的过程中：

\begin{equation} A_{x}(i, j) = \phi(x_{i}, x_{j},A_{x}’;\theta_{x})=\frac{\tilde{A}_{x}(i,j)\exp(\sigma(\theta^{T}_{x}[x_{i}|x_{j}]))}{\sum^{n}_{j=1}A_{x}’(i,j)\exp(\sigma(\theta^{T}_{x}[x_{i}|x_{j}]))} \end{equation}

拉普拉斯平滑卷积

用上标 \(k\) 来表示是第几层卷积： \begin{equation} X^{(k+1)} = \sigma[(1-\gamma)X^{(k)}\Theta^{(k)}_{n}+\gamma\tilde{A}^{(k)}_{x}X^{(k)}\Theta^{(k)}_{e}] \end{equation}

其中 \(\tilde{A}^{(k)}_{x}\) 分别表示行正则的拉普拉斯矩阵，\(\Theta^{(k)}=\{\Theta^{(k)}_{n}, \Theta^{(k)}_{e}\}\) 是神经网络中的参数。

行正则定义为 \(D^{-1}A\)，其中 \(D\) 是一个 \(D_{ii}=\sum_{j}A_{ij}\) 的对角矩阵。

图间卷积模块

中间层的特征表现为 \(X^{(k)}\in \mathbb{R}^{m\times d_{k}},Y^{(k)}\in \mathbb{R}^{n\times d_{k}}\)，则他们之间的亲和矩阵 \(C^{(k)}_{xy}\) 定义为：

\begin{equation} C^{(k)}_{xy}(i,j) = \exp (\frac{ {(X^{(k)}}^{T} WY^{(k)})_{ij}}{\delta}) \in\mathbb{R}^{m\times n} \end{equation}

其中 \(W\in \mathbb{R}^{d_{k}\times d_{k}}\) 是一个可训练的权重矩阵，相对的另一个矩阵也可以作为 \(C^{(k)}_{yx}\)，引出图间卷积学习模块为：

\begin{equation} X^{(k+1)}=[C^{(k)}_{xy}Y^{(k)}|X^{(k)}]\Theta^{(k)}_{xy} \end{equation}

\begin{equation} Y^{(k+1)}=[C^{(k)}_{xy}X^{(k)}|Y^{(k)}]\Theta^{(k)}_{yx} \end{equation}

匹配估计和损失函数

\begin{equation} \tilde{C}(i, j)=\exp(\frac{(\tilde{X}M\tilde{Y}^{T})_{ij}}{\delta’})\in \mathbb{R}^{m\times n} \end{equation}

这里的 \(i\) 和 \(j\) 分别表示了图一中 \(i\) 号节点和图二中 \(j\) 号节点的相似度，因为要做节点之间的一对一匹配，这就要求这个估计中每行都只有一个非零值，但是这种离散的方式会导致网络不可导。所以采用连续的 Sinkhorn 操作：

\begin{equation} C=\text{Sinkhorn}(\tilde{C}) \end{equation}

排列问题是一个典型的离散优化问题，因为不可导的原因，直接通过神经网络的梯度下降算法等不能解决，所以通过 Sinkhorn 算子¹对原来排列组合问题重新表示，其中这个 Sinkhorn 操作在最优传输理论中是非常重要的一个概念。

参照一份最优传输计算简介-机器之心可以了解大致的排列组合不可导转化问题。

另外，Gumbel-Sinkhorn 的基本思路是，一个排列结果实际上等于原序列乘以一个置换矩阵。而我们可以用 Sinkhorn 算子，以一种连续化的思路逼近这个置换矩阵。通过这种转化之后，排列问题就转化成了置换矩阵的学习问题。我们知道置换矩阵的特点是每行、每列都只有一个 1，其他元素都是 0。而 sinkorn 算子所做的事情就是把一个随机初始化的矩阵通过连续的计算过程转化成一个合适的置换矩阵，就可以进一步完成元素的排列了。

首先指数化整个矩阵，然后分别对行和列做归一化。不断重复这个过程就使得原来的随机初始化矩阵无限接近一个置换矩阵。

约束正则

\begin{equation} U_{ij,kl}=\left\{\begin{array}{cl}1 & \text{if}~i=k, j\neq l, or~i\neq k,j=l \\0 & \text{otherwise.}\end{array}\right. \end{equation}

其中，下标矩阵 \(U\in \mathbb{R}^{mn\times mn}\) 表示在点配对过程中，有多少冲突。一个理想的匹配应该是：

\begin{equation} \sum_{i,j}\sum_{k,l}U_{ij,kl}C_{ij}C_{kl} = 0 \end{equation}

那么冲突损失就可以写成：

\begin{equation} \mathcal{L}_{con}=\sum_{i,j}\sum_{k,l}U_{ij,kl}C_{ij}C_{kl} \end{equation}

交叉熵

用 \(P\in \mathbb{R}^{m\times n},P_{ij}\in \{0, 1\}\) 表示真正的点配对方式。 \begin{equation} \mathcal{L}_{sol} = -\sum_{i,j}P_{ij}\log(C_{ij}) + (1-P_{ij})\log(1-C_{ij}) \end{equation}

总的损失量加在一块：

\[\mathcal{L}=\mathcal{L}_{sol}+\lambda\mathcal{L}_{con}\]

其中 \(\lambda\) 用于表示点匹配错误率和点匹配冲突率的权重倾向。

---