Paper | Domain Agnostic Learning with Disentangled Representations

假设你有两批数据，一批是在游戏中模拟进行自动驾驶的场景训练数据，一批是真实世界中的任务数据，前一批我们有无尽二点标签，但是后一批的标签收集显然就需要很大的人力物力，所以我们希望在前面无尽的数据上训练好的模型能够经过一些调整直接解决后一批数据的任务，这也就是迁移学习要做的任务。

比较形式化的说法就是：迁移学习主要是为了能够弥合相同任务中的两批数据集的因为边缘分布不一致导致的协变量漂移的问题。基于一个假设：两批数据的边缘分布不同，但是条件概率分布是相同的，即 \(P(x\vert y)\) 还是相同的，同样的特征是要对应于同样的标签，但是 \(P(X)\) 是不相同的，因为数据分布是有些不同的。

所以针对这样的问题人们提出了一些解决方案：

通过学习一种嵌入表示方式能够弥补源域和目标域的协变量漂移问题。
通过对抗学习在保证源域性能情况下使得目标域和源域的中间特征变得难以辨别
如果在目标域标签可标记的情况下还可以引入主动学习：
1. 挑选那些最能让源域目标域辨别出错的样本
2. 挑选那些让源域上训练过的模型最不确定的样本

而实际进行迁移的时候也有几种不同的场景需求：

源域 \(\mathcal{S}\) 单 –> 目标域 \(\mathcal{T}\) 单
源域 \(\mathcal{S}\) 多 –> 目标域 \(\mathcal{T}\) 单
源域 \(\mathcal{S}\) 单 –> 目标域 \(\mathcal{T}\) 多

这篇文章要讨论的就是这第三个问题。

大致思路

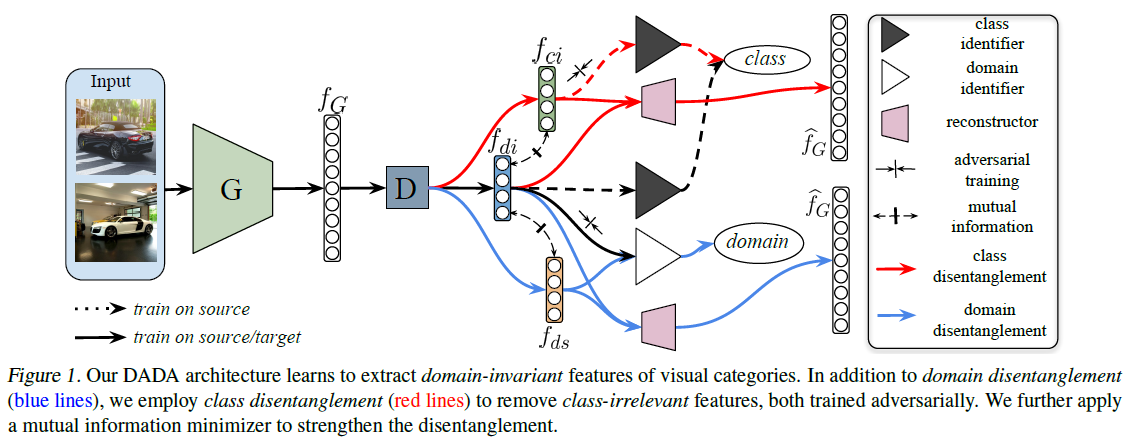
特征生成器 \(G\)
解耦器 \(D\)
域无关特征 \(f_{di}\)
域特定特征 \(f_{ds}\)
类别无关特征 \(f_{ci}\)
特征重建器 \(R\)
分类器 \(C\)

通过学习两个解耦对迁移任务进行改进，从域不变特征和类别特征通过互信息的水平分开。

变分自编码

\begin{equation} \mathcal{L}_{vae} = |\hat{f}_{G}-f_{G}|^{2}_{F} + KL(q(z|f_{G})|p(z)) \end{equation}

其中 \(p(z_{c})\) 是一个先验的分布，\(z\sim \mathcal{N}(0, I)\) 因为在损失函数中没有特别定义，而且特征量又是取自一个常规的分布，仅仅通过这个自编码器是不能把域不变和域相关的特征区分开来的。

类别解耦

\begin{equation} \mathcal{L}_{ce} = -\mathbb{E}_{(x*s, y_s)\sim \hat{D}_{s}}\sum^{K}_{k=1}\mathbb{1}[k=y_{s}]\log (C(f_{D})) \end{equation} 其中 \(f*{D}\in \{f*{di}, f*{ci}\}\)，用于去除类别不相关特征，通过交叉熵优化解耦器和分类器实现分类错误最小化。

第二步通过固定分类器，训练解耦器 \(D\) 生成类别无关的特征 \(f_{ci}\) 欺骗过分类器，可以通过负熵最小化实现：

\begin{equation} \mathcal{L}_{ent}=-\frac{1}{n_s}\sum^{n_s}_{j=1}\log C(f^{i}_{ci})-\frac{1}{n_t}\sum^{n_t}_{j=1}\log C(f^{j}_{ci}) \end{equation}

也就是使得 \(C(f^{i}_{ci})\) 在整体数据判断上都非常不确定。

域解耦

通过训练域鉴别器 DI 实现对域指定特征的解耦，也就是能够通过 \(f_{di}\) 或者 \(f_{ds}\) 来分别这些特征是来自源域 \(\mathcal{S}\) 的还是来自目标域 \(\mathcal{T}\) 的。

\begin{equation} \mathcal{L}_{DI} = -\mathbb{E}[l_{f}\log P(l_{f})] + \mathbb{E}(1-l_{f})[\log P(1-l_{f})] \end{equation}

这里的解耦器就是用于训练欺骗域鉴别器。

互信息最小化

可以把互信息 \(I(X;Y)\) 看成由于知道 \(y\) 值而造成的 \(x\) 的不确定性的减小(反之亦然)（即 \(Y\) 的值透露了多少关于 \(X\) 的信息量）¹。我们的目标当然是希望每种特征仅承担各自该承担的任务，也就是 \(f_{di},f_{ds}\) 之间以及 \(f_{di},f_{ci}\) 之间的互信息都要尽可能的小。 \begin{equation} I(\mathcal{D}_{x};\mathcal{D}_{f_{di}}) = \int_{\mathbb{X}\times\mathcal{Z}}\log \frac{d\mathbb{P}_{XZ}}{d\mathbb{P}_{X}\otimes\mathbb{P}_{Z}}d\mathbb{P}_{XZ} \end{equation} 其中 \(x\in\{f_{ds}, f_{ci}\}\)，\(\mathbb{P}_{XZ}\) 是 \((\mathcal{D}_{x},\mathcal{D}_{f_{di}})\) 的联合分布。\(\mathbb{P}_{X}=\int_{\mathcal{Z}}d\mathbb{P}_{XZ}\) 和 \(\mathbb{P}_{Z}=\int_{\mathcal{X}}d\mathbb{P}_{XZ}\) 是边缘分布，这也就是一个类似于贝叶斯概率的公式。但是这种计算复杂度过高，尤其是还用了张量积 \(\otimes\) 导致复杂度到 \(O(n^2)\)，所以参照 Mutual Information Neural Estimator（MINE）的做法进行了简化：

\begin{equation} I\hat{(X;Z)}_{n} = \sup_{\theta \in \Theta}\mathbb{E}_{\mathbb{P}^{(n)}_{XZ}}[T_{\theta}]-\log(\mathbb{E}_{\mathbb{P}^{(n)}\otimes\hat{\mathbb{P}^{(n)}_{Z}}}[e^{T_{\theta}}]) \end{equation} 可以利用神经网络 \(T_{\theta}\) 无偏地估计 \(n\) 个独立同分布样本的互信息。

然鹅在实际操作中，用的是更加简单的方式，\(I(X;Y)=\int\int \mathbb{P}^{n}_{XZ}(x,y)T(x,z,\theta)-\log(\int\int\mathbb{P}^{n}_{X}(x)\mathbb{P}^{n}_{Z}(z)e^{T(x,z,\theta)}\)，再进一步避免使用积分的形式，代码中是用蒙特卡洛采样的方式实现。

\begin{equation} I(X,Z) = \frac{1}{n}\sum^{n}_{i=1}T(x, z, \theta) - \log(\frac{1}{n}\sum^{n}_{i=1}e^{T(x, z’,\theta)}) \end{equation} 其中 \((x,z)\) 是从联合分布中采样得到的，\(z'\) 是从边缘分布中采样得到的。

改进批归一化

因为一般的批归一化是来自于同一批数据，假设都是类似的分布，但是在这里，目标域有多个域的数据（你还不知道哪个样本是来自哪个域的），所以批内肯定会出现（而且得是这样）协变量漂移的问题，不能简单通过批归一化，所以采用了环样的正则约束： \begin{equation} \mathcal{L}_{ring}=\frac{1}{2n}\sum^{n}_{i=1}(|T(x_i)|_{2}-R)^2 \end{equation} 但是还是容易出现一些模式坍塌的问题，如果这个学习到的 \(R\) 太小的话，所以做进一步改进就是引入 Geman-McClure 模型： \begin{equation} \mathcal{L}^{GM}_{ring}=\frac{\sum^{n}_{i=1}(|T(x_i)|_{2}-R)^2}{2n\beta +\sum^{n}_{i=1}(|T(x_{i})|_{2}-R)^2} \end{equation} 其中 \(\beta\) 是 Geman-McClure 模型的尺寸。

完整算法流程

wiki:互信息 ↩