因果分析 | 介绍 | Curiousity Hub

人们为了避免辛普森悖论等因为模型不明，混淆因素也一时无法确定而建立的各种分析方法，希望能够从大量的数据中找到满足控制变量条件的分析。主要包括建立新的表示符号，用以强调是在某个动作作用之后才有的某种结果，在这个理论基础上设计了因果图，分析方法和我们所认知的概率图分析等都比较一致。因果分析就是要在没有条件进行完全的控制变量的情况下进行数据分析，通过因果归纳得到因果结构，然后进行强度估计。

本文依照微软在 KDD 上的演示文稿整理部分和因果推理有关的内容如下。

符号约定

符号约定是为了区分因果性和原来我们熟悉的关联性模型的表达方式。\(P(Y\vert X)\) 和 \(P(Y\vert do(X))\) 表达的是不同含义，前者着重指根据数据观察得到的概率特征，而后者是指当施加某种干预会带来的某种结果，是着重表达因果性的。

Conditional Independence Assumption (CIA)
- 干预和变量不会相互影响对方的出现
Stable Unit Treatment Value (SUTVA) assumption
- 一个单元受到干预的影响和其他单元是否收到干预相互独立\(P(Y_i\vert do(T_i,T_j))=P(Y_i\vert do(T_i))\)
Common support
- 受到干预的一批变量和没有受到干预的一批变量应该是相似的
- 也就是协变量（covariates）应该有所重叠（带有某类如性别、年龄等属性的样本） \(0< P(T=1\vert X=x) < 1\)

结构因果模型

用概率图模型来表示因果关系，通过探索数据进行因果归纳建立图模型，然后通过大量的数据回测实现因果强度的推断。实际上，人们有时候会建立有人工干预的因果模型，这些因果模型能够比较好地表现数据中前后的因果关联。

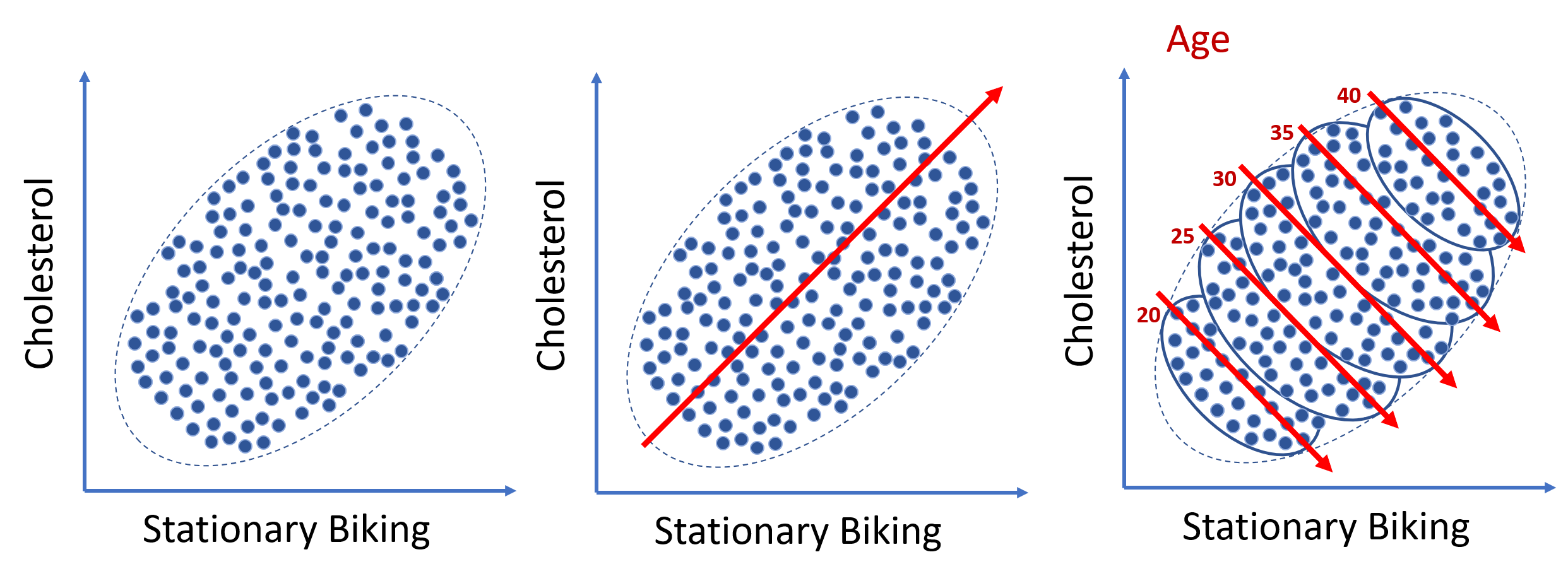
警告:只有正确的因果结构图才能带来正确的因果作用效应估计

要知道怎样进行良好的模型设计，如果建立 \(T\rightarrow Y\) 这样的联通就会导致错误的相关性分析，比如锻炼和胆固醇关系没有根据年龄这个同时作用在锻炼频率和胆固醇水平的混淆量（confounder）进行分层的话，就会得出错误的结论。但是如何对原始数据进行分组，这是具有挑战性的一点。

倾向评分匹配

因果分析方法的贡献在于能够在没有条件进行绝对的控制变量实验的情况下，直接通过对数据进行分层探索各个独立变量对于结果的影响程度。

因为在很多情况下，数据的维度都比较高，不会有特别分明的属性（例如年龄、性别等）便于进行针对属性进行分层。通过一些距离函数以无监督聚类的方案对原始数据进行分组，但是这样做的适应度有限，所以通过引入倾向性评分这个来进行数据的分组。

倾向性评分有效的原因在于，协变量相似的个体之间都比较可能有相似的分数，所有映射到相似分数的个体就比较有可能有相似的干预程度。

通过预测一个个体受到某个干预的可能性，可以作为分层的依据，这个分数估计先通过部分有监督的方法进行训练，然后对全部数据进行估计，得出他们的受到干预的倾向性评分 \(\hat{e}(\vec{x_i})\)，但是要对这个最终得分有个比较好的矫正对齐方案。也就是要有 \((100*p)\%\) 的样本有 \(p\) 的倾向性得分。然后依据倾向性得分计算样本之间的距离：\(\){\rm Distance}(\vec{x_i},\vec{x_k})=

\hat{e}(\vec{x_i})-\hat{e}(\vec{x_j})

\(\)

倾向性评分算不准是可以接受的，因为这是为了用于平衡协变量带来的分数，而不是真的直接确定干预作用关系。
倾向性评分准就很有问题了，这意味着没法把干预和协变量分开，因为任何观察到的影响都会来自干预或者相关的协变量。
- 解决方案：重新定义干预量，或者把问题陈述再泛化一下。

通过计算各个倾向性评分对原始样本进行分层。
计算不同层中对于收益影响的加权平均 \(ATT = \sum_{s\in strata}\frac{1}{N_{s,T=1}}(\bar{Y}_{s,T=1}-\bar{Y}_{s,T=0})\) 其中，\(\bar{Y}_{s,T}\) 是层 \(s\) 在 \(T\) 的干预下，\(N_{s,T=1}\) 是在层 \(s\) 中受到干预的样本数量。ATT 是指在对照组上控制量的影响差异（例如样本中有的对控制量起反应，有的不起反应）。

加权

数据集通常不会特别平衡，所以我们时常会根据其特征进行加权评估他们的收益效果，一些有效的加权方法可以改进这一问题。 \begin{equation} ATE = \frac{1}{N_{T=1}}\sum_{i\in {\rm Treated}}w_i Y_i-\frac{1}{N_{T=0}}\sum_{j\in {\rm Untreated}}w_j Y_j \end{equation} 其中，ATE 是指 Average Treatment Effect 表示控制组和对照组之间潜在的影响差异。

回归

通过回归探索某项干预在模型上的作用效果： \begin{equation} E(Y|X,T)=\alpha_1 X_1+\alpha_2 X_2+\alpha_3 X_3\dots +\alpha_n X_n+\alpha_T X_T \end{equation}

\(\alpha\) 越大，那么它们之间的因果性就越强。

回归的因果解释要满足下面几个假设：

模型正确性：如果用线性回归分析非线性的因果性就不行
共线性：如果协变量之间具有相关性，也不能得到准确的参数
可忽略性：如果漏了混淆变量可能会使分析无效

要非常仔细地设计模型，保证因果解释能力，避免出现共线性的协变量，确保所有相关的混淆变量都已经考虑到了。

双重鲁棒

在做模型分层的时候需要正确的模型说明
在做回归任务的时候也需要正确的模型指定

通过双重鲁棒采纳倾向性得分和回归方法中最好的组合，任意一个部分估计正确，都可以带来正确的结果，但是如果两个都估计的不好，那么双重鲁棒会带来更加严重的偏见。 \begin{equation} DR_1=\begin{cases} \frac{Y}{\hat{e}}-\frac{\hat{Y}_{T=1}(1-\hat{e})}{\hat{e}},& T=1 \
\hat{Y}_{T=1}, & T=0 \end{cases} \end{equation}

\begin{equation} DR_0=\begin{cases} \hat{Y}_{T=0}, & T=1 \
\frac{Y}{1-\hat{e}}-\frac{\hat{Y}_{T=1}(\hat{e})}{1-\hat{e}},& T=0 \end{cases} \end{equation}

最后计算所有研究样本的平均值 \(\bar{DR_1}\) 和 \(\bar{DR_0}\)，其中的差异也就是因果作用的影响程度。

合成控制

在一些场景中，所有的样本都受到某个干预的影响，比如政策、全球变暖等，我们需要建立生成控制来估计如果有一批样本没有受到干预的影响（因为这批样本在实际中并不存在）。

确定会有什么干预量
在干预来之前进行观测，拟合协变量和输出的关系
学习得到输出受干预量的影响

在出现干预以后：

通过前面学到的无干预模型估计假如没有干预会有什么样的输出
计算观测所得输出和无干预模型预测之间的差别

自然实验

通常，随机实验实验是检验因果关系的重要手段，通过近似随机算法获得某项干预对于输出的影响。为了达到这个目标，与其直接对数据进行可忽略性不如找到一个子集可以近似这样的实验。我们常见的做法有 A/B 测试、抽样、任意随机策略对干预的外部干扰等，只要源头没有受到这些常见的原因影响就可以使用它们。

工具变量

比如在霍乱源头分析的场景中，我们可以直接获得邻居因素对于得病的影响，而邻居关系和他们喝哪个自来水厂的水是基本相互独立的，也就是一种近似随机的关系，而自来水厂也不会直接影响他们是否得病，而是水污染让他们得病。

通过以上的例子进一步推广，可以抽象出工具变量，它们不会受到未观测的混销量影响，同时也不会直接影响到最终的输出。\((Z\amalg U)\) 其中 \(Z\) 为工具变量，\(U\) 为没有观测到的混淆变量，\((Z\amalg Y\vert T, U)\) 工具变量只能通过影响 \(X\) （也就是原因）影响到结果，而不能直接影响。因果影响可以通过下面的方式进行计算 \begin{equation} {\rm Causal~effect}(X\rightarrow Y)=\frac{T_{Z=1}-Y_{Z=0}}{X_{Z=1}-X_{Z=0}} \end{equation} 比如随机鼓励一些人去运动，我们可以观测得到运动对于胆固醇的影响程度。也就是通过工具变量来改变干预的分布，从而推断干预量在最终结果上的影响力。

回归中的不连续

这种不连续有时候是因为某些阈值带来的，但是在分界线两侧的样本应该是非常相似的，所以通过随机实验把他们放到另外一侧也是可行的。

回归中的不连续确定了实验组和对照组之间的任意边界，衡量了边界处差异作为对于最终结果影响程度。

反驳

通过随机增加一些协变量放入数据，再重新进行分析，如果因果估计没有改变，也就是这个当前的模型没有被驳倒。
随机或者打乱我们干预，重新进行因果分析，如果没有使分析结果改变，没有被驳倒。
把数据分成很多子集，进行分析，在各个子集内部没有明显差异，没有被驳倒。
测试协变量是否平衡。

总结

建模->归纳->估计->反驳

用多种方法验证
模型不要太过复杂