主动学习

主动学习是指通过自动的机器学习算法，从数据集中自动挑选出部分数据请求标签，在统计上也称为查询学习或者最优实验设计。主动学习通过设计合理的查询函数，不断从未标注的数据中挑选出数据加入标注后放入训练集。有效的主动学习数据选择策略可以有效地降低训练的代价并同时提高模型的识别能力。赋予你的模型好奇心，让其有一些如何去学习的智能。

主动学习概括

主动学习主要解决的问题是：

1. 标注任务的成本较高
2. 需要多少标注数据才能满足学习任务

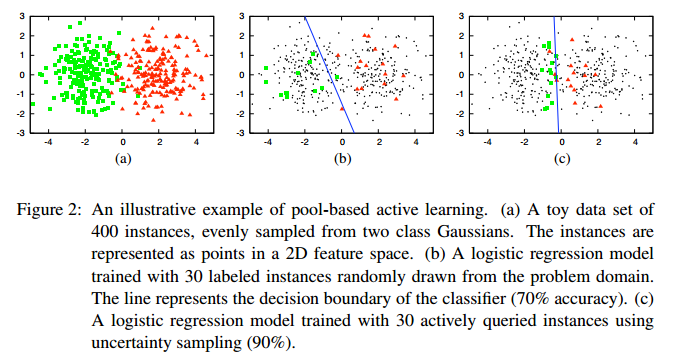
主动学习和监督学习、半监督学习的主要区别在监督学习和半监督学习中，人们都是从数据集中随机选取一部分数据进行标注，而主动学习是通过让模型主动去探索未标注的数据，从中选出有代表性的未标注数据提交给专家，然后由专家标注完成以后再放入训练数据集中。

一般的主动学习步骤¹为：

• 每轮开始的时候都有一个当前的模型（可以是预训练的或者根据已有模型训练的）
  1. 确定一个询问选择策略（query selection strategies）
  2. 找出最有信息量的样本
  3. 通过专家对数据进行标注
  4. 将新标注的数据加入到训练数据集中
  5. 基于当前的数据再训练模型
• 直到模型的性能达到目标条件或者已经没有条件再去标注数据了

但是在确定是否使用主动学习之前需要明确以下几个关键点：

1. 主动学习中的标签是否可获得
2. 是否已经有算法可以处理这类问题
3. 用什么指标来衡量样本的难度
4. 如何准备一套完整的系统接口来实现这一个过程

主动学习的场景

Membership Query Synthesis

生成一个询问，并请求这个样本的标签，这个样本可能是未标注数据中的任意一个，甚至是从头生成的，反正这些数据一般不是简单的服从一个自然分布的随机。

这会遇到比较复杂的情况，也就是它提出的需要标注的数据可能对于人而言看起来毫无意义，也就是无法标注的问题。

Stream-Based Selective Sampling

基于流的有选择性地选择目标，这种通常是假设会有大量廉价的无标签数据。它将采样一个无标签的数据，然后决定是要询问它的标签还是忽略它，通常基于下面的两个度量：

1. 更高的信息量：选择这些具有高信息量的数据
2. 不确定性原则：只选择落在这种不确定域之中的数据

实际上的数据来源可能是连续语音数据的某一段，文字歧义消除，或者确定上下文中的关系等。

Pool-Based Sampling

基于池的采样，假设能够一次性获得大量未标注的数据，并且能够进行同时处理。可以对数据池中的数据进行信息量排序，这样可以直接采用最有信息量的数据进行分析。

实际中的数据来源可能是癌症相关的数据，图像识别，分类标注，视频的分类识别等。

基于流的场景下，数据是顺序来到的，一次性不会有全局的视野，而基于池的则是更加常见的做法可以一次性对所有数据的信息量进行分析。但是有的时候因为数据的生成情况或者计算带宽内存等的限制，人们还是不得已还是要使用基于流的场景。

主动学习询问算法

所有的主动学习算法都需要合适的询问算法。

基于不确定性的选择

挑选出当前的模型最没有信心的样本，通常越靠近超平面分类边缘的样本就越容易不确定。根据样本的标签分布也有几种选择方法：

• Least Confident：\(x^{*}_{LC}=\text{argmax}_{x}1-P_{\theta}(\hat{y}|x)\) 其中 \(\hat{y}=\text{argmax}_{y}P_{\theta}(y\vert x)\)，也就是根据当前的模型状态估计得到标签量次数最少的样本将会得到更多的光顾
• Smallest Margin: \(x^{*}_{SM}=\text{argmin}_{x}P_{\theta}(\hat{y}_{1}|x)-P_{\theta}(\hat{y}_{2}|x)\) 其中 \(\hat{y}_{1}\) 和 \(\hat{y}_{2}\) 是当前样本最高可能性的两个样本。
• Label Entropy：\(x^{*}_{LE}=\text{argmax}_{x}-\sum_{i} P_{\theta}(y_{i}|x)\) 其中 \(y_{i}\) 表示当前这个样本所有可能的标签

基于委员会的选择

主动学习方法选择一定数量的模型构成委员会，对未标注的数据进行处理，挑选出所有未标记数据中各个模型意见最不一致的样本。一个准确衡量意见不一致程度的方法就是投票熵（Vote Entropy）

\[x^{*}_{VE} = \text{argmax}_{x}-\sum_{i}\frac{V(y_{i})}{C}\log \frac{V(y_{i})}{C}\]

其中，\(y_{i}\) 表示了所有可能的标签，\(V(y_{i})\) 表示了标签 \(y_{i}\) 所得到的票数 \(C\) 表示了委员会的规模。

在主动学习的场景中，需要同时准备多个计算模型，这回带来比较高的计算复杂度，所以引入了熵值装袋查询（EBQ）简化了计算过程，另外自适应不一致最大化（AMD）在前者的基础上还做了改进，避免了维数灾难的问题。

基于边缘的选择

以二分类任务举例的话，越靠近分类面的样本就越有可能被选择。

但是其前提是分类模型可以给出样本到分类面的距离，

• MS：仅仅简单的选择距离分类界面最近的样本
• MCLU：选择离分类面最远的两个最可能的样本的距离差作为判断依据

在多种类别混合的情况下，MCLU 可以选择最不确定的样本。再引入多样性准则和样本间相似度从已经选择的训练集中剔除冗余的样本。

基于后验概率的选择

根据样本预测所得的后验概率值的大小对候选样本集进行排序，通过分析后验概率的变化或每个候选样本归属的每类分布情况，确定出模棱两可的区域，从中选取样本构成训练集。

• Kullback-Leibler 最大化：相对熵最大化 \(x^{*}_{KL}=\text{argmin}_{x_{i}\in U}\sum_{w\in U}\frac{1}{(u-1)}KL(p^{+}(w \vert x)\|p(w \vert x))p(\hat{y}=w\vert x_{i})\)
• Breaking Ties：

主动学习的方向

近些年来大量的深度学习模型取得性能在很大程度上得益于良好的公开数据集，人们习惯性地把大量数据打上标签，并分为训练集、验证集、测试集。但是在更多的场景中，或者更加实际的问题中，我们往往不具备这样的条件，面对常见场景的时候，我们在分类上有 ImageNet，在检测上有 COCO，在人体姿态估计上有 MPII、COCO，在自动驾驶上有 KITTI 等等，但是实际的情况是，面对癌症数据，没有可用的预训练模型，没有数据集标准，甚至标注也难以进行，面对大型垃圾分类任务，都已经远远超出了原来文章所设定的场景，人们为了在某个数据集上有了更好的准确率时可能根本不会想起这个问题。再高几个百分点，是有点意义，但是相对而言，让这些模型流动到更大型的场景中去，需要的是我们需要在高效的自动化算法中确定这个学习问题所要优化的目标和更快的方式。

提出更好的主动选择策略

• Active Learning for Human Pose Estimation(ICCV2017) 作者表示这是第一次这样深入地应用主动学习到人体姿态估计的领域中里，根据现有模型的回归能力，用多峰熵来对输出的 haetmap 进行打分，对于获得的 heatmap 给出不确定度的分值。 基于 \(模型对当前样本估计的不可靠度 \times 当前样本的模型影响力（代表性）+ 模型对当前样本估计的可靠程度 \times 模型对当前样本的不确定度\) 对未标记的样本进行打分排序，选出最值得标记的样本进行人工标记，然后再基于更新的数据集训练模型。

  其中，多峰熵（Multiple Peak Entropy，MPE）的定义在下面两步，先用类似于 Sigmoid 函数确定各个关键点的标签和坐标：

  \[\operatorname{Prob}\left(I_{i}, m, p\right)=\frac{\exp b_{p}^{t}\left(Y_{p}=z_{m} | I_{i}\right)}{\sum_{m} \exp b_{p}^{t}\left(Y_{p}=z_{m} | I_{i}\right)}\]

  然后基于估计结果衡量：

  \[C_{M P E}\left(I_{i}, p\right)=\sum_{m}-\operatorname{Prob}\left(I_{i}, m, p\right) \log \operatorname{Prob}\left(I_{i}, m, p\right)\]

  为了表示当前这个估计结果是那种几个可以明显区分的独立峰还是那些比较低矮比较模棱两可的估计结果。

  另外影响力这一步，就看这个图像是不是像大多数良好的识别场景一样，图像比较干净，然后人也摆的比较正等等，所以就通过这个图像是不是和数据集中较多的图像相似来确定这个图像的相似度：

  \[C_{I N F}\left(I_{i}\right)=\frac{1}{\left|U_{t}\right|-1} \sum_{I_{j} \in U_{t} \backslash I_{i}} d\left(I_{i}, I_{j}\right)\]

  基于这种探索过数据集分布和模型输出的主动学习策略，确实可以提高估计准确度，因为挑选出的数据是通例和难例，这和学生做题也比较像，常规题能拿的分数不要丢，难题挑出来重点攻克，偏题怪题就随个人能力了。

• Learning Loss for Active Learning（CVPR2019） 提出与任务无关的主动学习策略，用一个只包括一层卷积池化全连接的简单神经网络和解决任务的模型同步成长。根据模型的特征层输出对模型在某个样本上可能有的 Loss 进行预测，这样一同成长的主动学习模块，通过和模型一起探索未标注的数据猜测模型对哪些样本不擅长需要人们协助给出标签来学习的。相当于模型的一颗好奇心。

  在训练策略上，解决任务模型和 Loss 预测模型的 Loss 是被加在一起输出的：

\begin{equation} L_{\text {target }}(\hat{y}, y)+\lambda \cdot L_{\operatorname{loss}}(\hat{l}, l) \end{equation}

但是，任务执行模型的 Loss 会随着训练的进行而下降的，那么预测 Loss 的模块就算什么也学不到，它的 Loss 也会随着下降，所以需要排除任务执行模型的 Loss 下降影响，增加另外的模块：

\[\begin{aligned} L_{\operatorname{loss}}\left(\hat{l}, l^{p}\right)=\max &\left(0,-\mathbb{1}\left(l_{i}, l_{j}\right) \cdot\left(\hat{l}_{i}-\hat{l}_{j}\right)+\xi\right) \\\\ & \text { s.t. } \quad \mathbb{1}\left(l_{i}, l_{j}\right)=\left\{\begin{array}{ll}{+1,} & {\text { if } l_{i}>l_{j}} \\\\ {-1,} & {\text { otherwise }}\end{array}\right.\end{aligned}\]

把训练过程中 Batch 对半，然后排除两个 batch 之间的任务执行模型的 Loss 下降，凸显出 Loss 预测模型的能力变化，其中 \(\xi\) 表示是一个常数间隔（参考 SVM 中的间隔定义）。最终完整的组合 Loss 计算如下：

\begin{equation} \begin{array}{c}{\frac{1}{B} \sum_{(x, y) \in \mathcal{B}^{*}} L_{\text {daget }}(\hat{y}, y)+\lambda \frac{2}{B} \cdot \sum_{\left(x^{p}, y^{p}\right) \in \mathcal{B}^{s}} L_{\text {loss }}\left(\hat{p}, l^{p}\right)} \\ {\hat{y}=\Theta_{\text {taxget }}(x)} \\ {\text { s.t. } \quad \hat{l}^{\hat{p}}=\Theta_{\text {losse }}\left(h^{p}\right)} \\ {l^{p}=L_{\text {target }}\left(\hat{y^{p}}, y^{p}\right)}\end{array} \end{equation}

更高效的人机交互方式

更好的数据集模型管理

---