蒙特卡洛搜索树

March 07, 2018

2018   ·   Monte Carlo Tree   BasicModel   KL 距离   相对熵   Relative Entropy     ·   机器学习  

蒙特卡洛方法是通过统计的方式进行问题求解，最简单的例子就是使用蒙特卡洛方法估算\(\pi\)值。

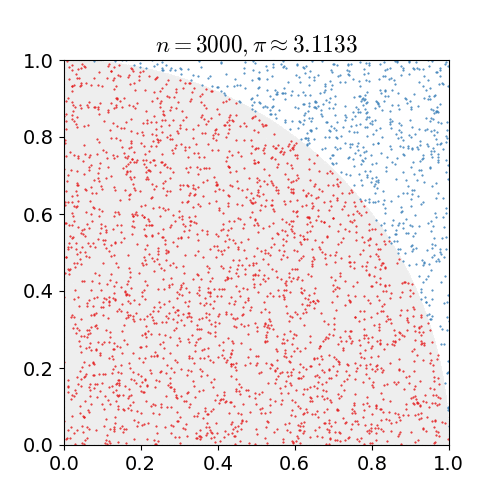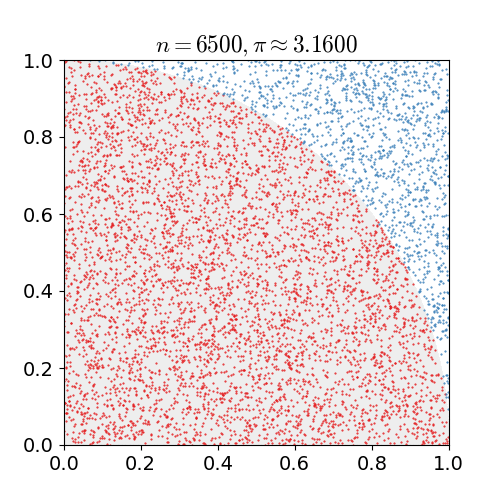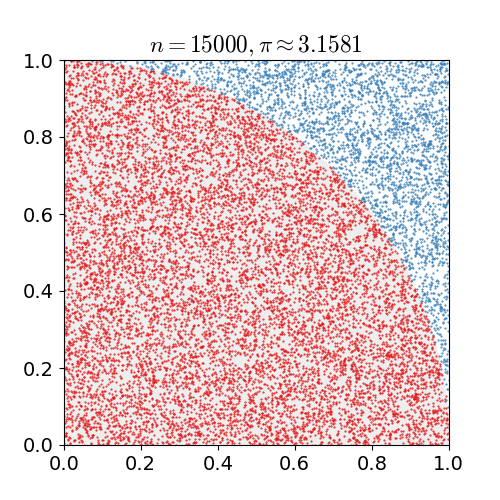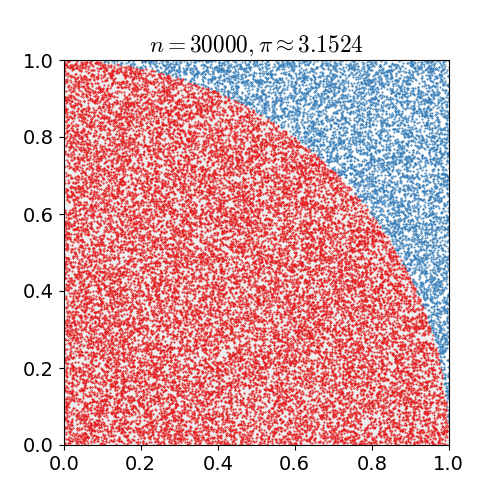
估算\(\pi\)值的代码也非常简单：

import random
exm_turn = 100000

counter = 0
for _ in range(exm_turn):
    x = random.uniform(-1, 1)
    y = random.uniform(-1, 1)
    # dropped in circle
    if x**2 + y**2 < 1:
        counter = counter + 1
print("pi:{0}".format((4 * counter / exm_turn)))

但是很容易看出这样估算的值不仅不准确，计算速度还特别慢，但是如果换一个场景，我们并不需要非常精确的数值，但是准确的计算量又过于庞大，那么用这种基于概率的计算方式（猜）通常能更好地达到计算结果。

发展过程

在博弈论中，参与博弈的个体和他们选择的方案带来的结果都可以列成一个表格进行分析，其中有一种算法为极小值极大化，这种算法通常用在零和博弈1，即参与博弈的双方的利益之和为零的博弈，如果一方得利，那另一方一定受损。极大值极小化是一种找出失败得最大可能性中得最小值的算法。

  • 1928年： John von Neumann的极大极小定理为对抗树搜索方法铺平了道路，这些方法几乎是自成立以来就形成了计算机科学和人工智能决策的基础。
  • 20世纪40年代： Monte Carlo（MC）方法被形式化为通过使用随机采样来处理不适合树搜索的不太明确的问题的方法。
  • 2006年： RémiCoulomb和其他研究人员将这两个想法结合起来，为移动计算机Go的计划提供了一种新的方法，现在称为MCTS。Kocsis和Szepesvári将这种方法形式化为UCT算法。

应用场景

在很多过程完全透明的游戏中能够很好应用，像是剪刀石头布，跳棋，翻转棋，象棋和围棋等这一类的每一步都很清楚，所有过程都直接展现给所有玩家的游戏。因为所有的步骤都是百分之百确定的。

算法说明

统计置信区间

我们将Upper Confidence bound applied to Trees（UTC）应用于此处来描述蒙特卡洛搜索树。

在开局时，我们通过对所有的可能的操作都构造一个置信区间： \begin{equation} \overline{x}_{i}\pm C\times \sqrt{\frac{2\ln n}{n_{i}}} \end{equation} 其中：

  • \(\overline{x}_{i}\)：操作\(i\)的平均付出
  • \(n_{i}\)：操作\(i\)进行的次数
  • \(n\)：所有的操作次数

根据当前所处的状态，我们可以根据自然情况构造出一个分布，之后随着我们的探索这个分布会逐渐接近真实的分布状态。

Bandit

选择比努力更重要，一般人做出了错误的决定都会感到后悔，而这个后悔的程度也可以进行度量，而且在经济学上也是有一个类似的名词称为机会成本，即选择某一个项目时的成本就是为了选择这个项目而放弃的其他项目中可获得最大的那个收益2。类似的，如果我们做的选择是收益最大的，那就没什么好后悔的，但是如果不是最好的决定，那就会有点失望了。

定义后悔函数3：

\begin{equation} \mu^{*}-\mu_{j} \sum^{K}_{j=1} \mathbb{E}[T_{j}(n)]\quad where\quad \mu^{*} \stackrel{def}{=} \max_{1\leq i\leq K}\mu_{i} \end{equation}

我们将这个多臂问题的解决方案加入到蒙特卡洛搜索树的算法中去4。以上的这个后悔函数虽然是有很好的表现能力但是计算起来过于复杂了，经过证明实际上可以用更加简单的方式来进行类似的算法实现。

TODO:完成Bandit的说明

树形搜索

下图中，wins/number表示对应节点（奖励多少次/被尝试了多少次）

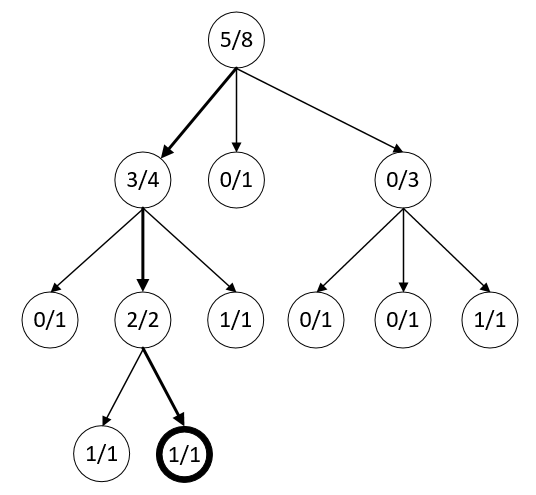
title:从根节点（初始状态）开始每次都选择最优的子节点（下一步），直到抵达下一步信息完全未知的一个节点

到达当前标粗的节点之后，所有用于估计的信息就都没有了，这样只能以随机的方式进行一次探索了，也就是随便做一步看看反应如何，这里说的随便做一步是出于简化描述考虑，实际上在对于下一步的选择可能是有权重偏好的，但也还是有随机性存在其中。

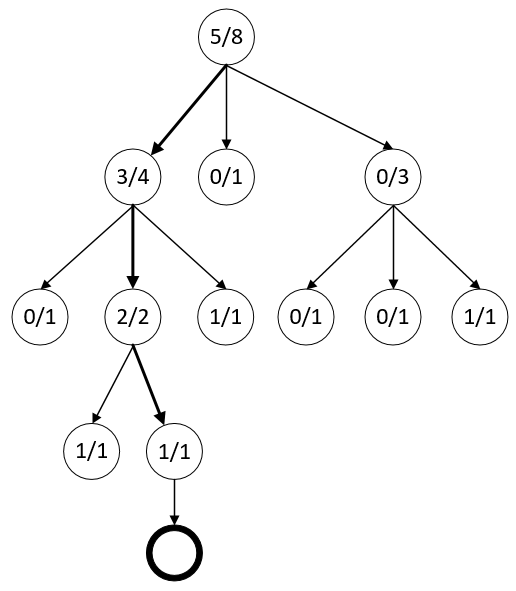
title:通过这种方式这棵决策树就得到了扩展

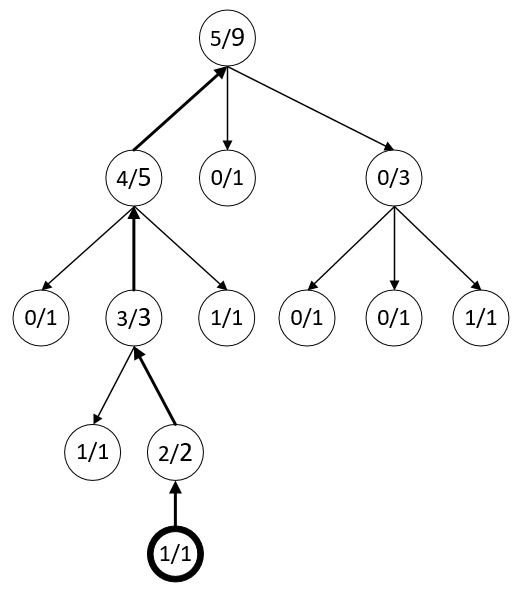
然后再观察这一步操作的反馈

title:根据得到的结果更新树的内容

代码样例5

先新建一个游戏操作的类，提供合法移动和游戏状态等。

class Board(object):
    def start(self):
        # Returns a representation of the starting state of the game.
        pass

    def current_player(self, state):
        # Takes the game state and returns the current player's
        # number.
        pass

    def next_state(self, state, play):
        # Takes the game state, and the move to be applied.
        # Returns the new game state.
        pass

    def legal_plays(self, state_history):
        # Takes a sequence of game states representing the full
        # game history, and returns the full list of moves that
        # are legal plays for the current player.
        pass

    def winner(self, sate_history):
         # Takes a sequence of game states representing the full
        # game history.  If the game is now won, return the player
        # number.  If the game is still ongoing, return zero.  If
        # the game is tied, return a different distinct value, e.g. -1.
        pass

完成了游戏操作设计之后开始完成蒙特卡洛搜索树的内容：

class MonteCarlo(object):
    def __init__(self, board, **kwargs):
        # Takes an instance of a Board and optionally some keyword
        # arguments.  Initializes the list of game states and the
        # statistics tables.
        pass

    def update(self, state):
        # Takes a game state, and appends it to the history.
        pass

    def get_play(self):
        # Causes the AI to calculate the best move from the
        # current game state and return it.
        pass

    def run_simulation(self):
        # Plays out a "random" game from the current position,
        # then updates the statistics tables with the result.
        pass

然后对其中的接口进行一个个实现：

class MonteCarlo(object):
    def __init__(self, board, **kwargs):
        self.board = board
        self.states = []

    def update(self, state):
        self.states.append(state)

UCT算法依赖于从当前的状态出发进行很多次测试：

import datetime

class MonteCarlo(object):
    def __init__(self, board, **kwargs):
        # ...
        seconds = kwargs.get('time', 30)
        self.calculation_time = datetime.timedelta(seconds = seconds)

    # ...

    def get_play(self):
        begin = datetime.datetime.utcnow()
        while datetime.datetime.utcnow() - begin < self.calculation_time:
            self.run_simulation()

在上面的代码中还规定了进行模拟的运行时间，在这个给定时间内就可以一直进行问题的搜索和求解。

from random import choice

class MonteCarlo(object):
    def __init__(self, board, **kwargs):
        # ...
        self.max_moves = kwargs.get('max_moves', 100)

    # ....

    def run_simulation(self):
        states_copy = self.states[:]
        state = states_copy[-1]

        for t in range(self.max_moves):
            legal = self.board.legal_plays(states_copy)

            play = choice(legal)
            state = self.board.next_state(state, play)
            state_copy.append(state)

            winner = self.board.winner(states_copy)
            if winner:
                break

在上面的部分用了状态集的拷贝是为了不影响真正记录步骤的内存空间中的记录，然后进行模拟演算未来步骤之后要进行记录重演的结论了

class MonteCarlo(object):
    def __init__(self, board, **kwargs):
        # ...
        self.wins = {}
        self.plays = {}

    # ...

    def run_simulation(self):
        visited_states = set()
        states_copy = self.states[:]
        state = states_copy[-1]
        player = self.board.current_player(state)

        expand = True
        for t in range(self.max_moves):
            legal = self.board.legal_plays(states_copy)

            play = choice(legal)
            state = self.board.next_state(state, play)
            states_copy.append(state)

            # 'player' here and below refers to the player
            # who moved into that particular state
            if expand and (player, state) not in self.plays:
                expand = False
                self.plays[(player, state)] = 0
                self.wins[(player, state)] = 0

            visited_states.add((player, state))

            player = self.board.current_player(state)
            winner = self.board.winner(states_copy)
            if winner:
                break

        for player, state in visited_states:
            if (player, state) not in self.plays:
                continue
            self.plays[(player, state)] += 1
            if player == winner:
                self.wins[(player, state)] += 1

我们通过建立wins和plays的字典，用于追踪所有的游戏行为轨迹，这个字典是用的set的数据结构，用来保证相同的状态动作集可以被修改。

from __future__ import division
# ...

class MonteCarlo(object):
    # ...

    def get_play(self):
        self.max_depth = 0
        state = self.states[-1]
        player = self.board.current_player(state)
        legal = self.board.legal_plays(self.states[:])

        # Bail out early if there is no real choice to be made.
        if not legal:
            return
        if len(legal) == 1:
            return legal[0]

        games = 0
        begin = datetime.datetime.utcnow()
        while datetime.datetime.utcnow() - begin < self.calculation_time:
            self.run_simulation()
            games += 1

        moves_states = [(p, self.board.next_state(state, p)) for p in legal]

        # Display the number of calls of 'run_simulation' and the
        # time elapsed.
        print(games, datetime.datetime.utcnow() - begin)

        # Pick the move with the highest percentage of wins.
        percent_wins, move = max(
            (self.wins.get((player, S), 0) / self.plays.get((player, S), 1),
            p) for p, S in moves_states
        )

        # Display the stats for each possible play.
        for x in sorted(
            ((100 * self.wins.get((player, S), 0) / self.plays.get((player, S), 1),
            self.wins.get((player, S), 0),
            self.plays.get((player, S), 0), p)
            for p, S in moves_states),
            reverse = True
        ):
            print("{3}: {0:.2f} % ({1} / {2})".format(*x))

        print("Maximum depth searched:", self.max_depth)

        return move

我们在get_play中增加提早结束的判断，如果没有步骤了或者只有一步可走了，那就返回。然后增加了一些调试信息输出，最后输出赢面最高的步骤，也就是赢的频率最高的那个操作。

但是到目前为止还不够完整，因为程序用的还是纯随机的表现，我们需要实现UCB1算法，把哪些存在状态表里的信息都利用起来。

# ...
from math import log, sqrt

class MonteCarlo(object):
    def __init__(self, board, **kwargs):
        # ...
        self.C = kwargs.get('C', 1.4)

    # ...

    def run_simulation(self):
        # A bit of an optimization here, so we have a local
        # variable lookup instead of an attribute access each loop
        plays, wins = self.plays, self.wins

        visited_states = set()
        states_copy = self.states[:]
        state = states_copy[-1]
        player = self.board.current_player(state)

        expand = True
        for t in range(1, self.max_moves + 1):
            legal = self.board.legal_plays(states_copy)
            moves_states = [(p, self.board.next_state(state, p)) for p in legal]

            if all(plays.get((player, S)) for p, S in moves_states):
                # If we have states on all of the legal moves here, use them
                log_total = log(
                    sum(plays[(player, S)] for p, S in moves_states))
                value, move, state = max(((wins[(player, S)] / plays[(player, S)]) +
                self.C * sqrt(log_total / plays[(player, S)]), p, S)
                for p, S in moves_states)
            else:
                # Otherwise, just make an arbitrary decision.
                move, state = choice(moves_states)

            states_copy.append(state)

            # ‘player' here and below refers to the player
            # who moved into that particular state.
            if expand and (player, state) not in plays:
                expand = False
                plays[(player, state)] = 0
                wins[(player, state)] = 0
                if t > self.max_depth:
                    self.max_depth = t

            visited_status.add((player, state))

            player = self.board.current_player(state)
            winner = self.board.winner(states_copy)
            if winner:
                break

        for player, state in visited_states:
            if (player, state) not in plays:
                continue
            plays[(player, state)] += 1
            if player == winner:
                wins[(player, state)] += 1

上面代码中最大的变化就是（在选择下一步操作前）检查所有合法操作的结果都在行动字典里了，如果它们还没有都在，就使用原本的随机选择下一步操作。但是如果统计信息覆盖了全部操作结果的话，那么根据置信区间的操作公式，具有最高值的那一步会被选择。这个公式结合两个部分，第一部分是得到赢率，第二部分是缓慢强化的特定形式，因为有些操作是始终被忽略的，但是这未必是好事。所以如果一个胜率不佳的操作在一定长时间内始终没有被选择的话，就会被再次选中。这个特定的间隔可以根据上面在__init__中被初始化的C进行调整，C越大就表示鼓励越多的探索。还有，当添加了新的节点，并且其深度超过了前面的self.max_depth时，前面的self.max_depth的属性就会被更新。

通过这个接口结构，可以尝试着做一个自己的游戏智能了吧。

TODO: 实现一个类似的游戏

更多阅读

KL距离

KL距离是是Kullback-Leibler差异（Kullback-Leibler Divergence）的简称，也叫做相对熵（Relative Entropy）。它衡量的是相同事件空间里的两个概率分布的差异情况。其物理意义是：在相同事件空间里，概率分布\(P(x)\)的事件空间，若用概率分布\(Q(x)\)编码时，平均每个基本事件（符号）编码长度增加了多少比特。我们用\(D（P\parallel Q）\)表示KL距离，计算公式如下：

\begin{equation} D(P\parallel Q) = \sum_{x\in X}P(x)\log \frac{P(x)}{Q(x)} \end{equation}

当两个概率分布完全相同时相对熵为0。所以我们通常用相对相对熵来衡量两个分布的差异程度。这个KL距离并不是常用意义上的距离，任意两个分布\(P\)和\(Q\)中，KL距离是不对称的即\(D(P\parallel Q) \neq D(Q\parallel P)\)。

补充资料

  1. https://en.wikipedia.org/wiki/Zero-sum_game ↩

  2. http://wiki.mbalib.com/wiki/%E6%9C%BA%E4%BC%9A%E6%88%90%E6%9C%AC ↩

  3. Auer, P., Cesa-Bianchi, N., & Fischer, P. (2002). Finite-time analysis of the multiarmed bandit problem. Machine learning, 47(2-3), 235-256. ↩

  4. Kocsis, L., & Szepesvári, C. (2006, September). Bandit based monte-carlo planning. In European conference on machine learning (pp. 282-293). Springer, Berlin, Heidelberg. ↩

  5. https://jeffbradberry.com/posts/2015/09/intro-to-monte-carlo-tree-search/ ↩



Enjoy Reading This Article?

Here are some more articles you might like to read next:

  • Word 排版技巧
  • 一个3D模型（译）
  • Black First Won
  • Extend LLMs Context Window
  • a post with images