频繁模式挖掘

在很多时候我们会关注两个或多个对象同时出现的频率，这些相关性往往意味着某种行为特征。例如我们可以根据网站的日志找到网站中某些的网页经常被用户访问到，这些频繁性提供了用户浏览习惯的线索，有助于提高浏览的体验。其中非常典型的应用就是购物篮分析（market basket analysis）可以通过用户经常购买的物品集合找到人们经常一起买的物品集合。之后可以提取出这些物品的关联规则（association rule）比如可以发现啤酒和尿布经常会被人组合购买，从而将这些物品放在邻近的地方销售会有更好的效果。

伯努利变量

伯努利变量其实和one-hot¹一样，根据标签的数量建立一个one-hot向量，\(X\)为一个定义域为\(\{ a_1,a_2,\dots,a_m \}\)的类别属性。可以将\(X\)建模为一个m维的随机变量\(\mathbf{X}=(A_1,A_2,\dots,A_m)^T\)，其中每一个\(A_i\)是一个参数为\(p_i\)（代表观察到符号\(a_i\)）的伯努利变量。因为是表示属性，所以一次只能取一个值。若\(X=a_i\)，则\(\mathbf{X}=e_i\)，其中\(e_i\)是第\(i\)个标准基向量的\(e_i\in \mathbb{R}^m\)：

\begin{equation} e_i=(\underbrace{0, \dots, 0}_{i-1}, 1, \underbrace{0, \dots, 0}_{m-i})^T \end{equation}

m维随机伯努利变量\(\mathbf{X}\)的值域由m个不同的向量值\(\{e_1, e_2, \dots, e_m\}\)构成，且\(\mathbf{X}\)的概率质量函数为：

\begin{equation} P(\mathbf{X}=e_i)=f(e_i)=p_i \end{equation}

项繁集和事务标识符集

令\(\mathcal{I}=\{x_1, x_2, \dots, x_m\}\)为一组称为项(item)的元素集合例如超市中售卖的所有产品的集合。集合\(X\subseteq \mathcal{I}\)称为项集。一个基数为k或者大小为k的项集称为k项集，用\(\mathcal{I}^{(k)}\)表示所有k项集。

令\(\mathcal{T}=\{t_1, t_2, \dots, t_n\}\)为另一个所谓的事务标识符(tid)构成的集合。事务（transaction）是一个形如\(\langle t, X\rangle\)的元组，其中\(t\in \mathcal{T}\)是一个独一无二的标识符，\(X\)是一个项集。事务的集合\(\mathcal{T}\)可以代表超市中的所有客户等。方便起见可以用\(t\)来表示一个\(\langle t, X\rangle\)。

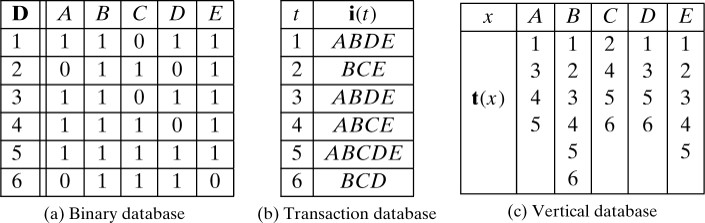
一个二元数据库\(\mathbf{D}\)表示了事务标识符集和项集之间的二元关系。

支撑集和频繁项集

数据集\(\mathbf{D}\)的一个项集\(X\)的支撑（support），表示为\(\sup(X,\mathbf{D})\)，即\(\mathbf{D}\)中所有包含\(X\)的事务的数目：

\[\sup(X, \mathbf{D})=\mid \{t\mid \langle t, \mathbf{i}(t) \rangle \in \mathbf{D}且X\subseteq \mathbf{i}(t)\}\mid=\mid\mathbf{t(X)}\mid\]

\(X\)的相对支撑（relative support）即包含\(X\)的事务的比例：

\[r\sup(X,\mathbf{D})=\frac{\sup(X,\mathbf{D})}{\mid D\mid}\]

它是对包含\(X\)的项的联合概率的一个估计。

关联规则

关联规则（association rule）是一个表达式\(X~^{\underrightarrow{s,c}} ~Y\)，其中\(X,Y\subseteq \mathcal{I}\)且\(X\cap Y=\emptyset\)。此处用\(XY\)表示项\(X\cup Y\)。规则的支撑是指\(X\)和\(Y\)同时出现的事务的总数：

\[s=\sup(X\longrightarrow Y)=\mid \mathbf{t}(XY)\mid = \sup(XY)\]

规则的相对支撑（relative support）定义为\(X\)和\(Y\)同时出现的事务的比例，它提供了对\(X\)和\(Y\)的联合概率的估计：

\[r\sup(X\longrightarrow Y)=\frac{\sup(XY)}{\mid\mathbf{D} \mid}=P(X\wedge Y)\]

一条规则的置信度（confidence）是一个事务包含\(X\)的情况下也包含\(Y\)的条件概率：

\[c=conf(X\longrightarrow Y) = P(Y\mid X) = \frac{P(X\wedge Y)}{P(X)}=\frac{\sup(XY)}{\sup(X)}\]

根据规则支撑和置信度的定义，可以观察到，为了生成频繁且高置信度的关联规则，首先要枚举所有的频繁项集及其支撑值。

暴力枚举

首先要做候选生成，因为一个集合\(\mathcal{I}\)有\(2^{\mid \mathcal{I} \mid}\)个子集也就有\(2^{\mid \mathcal{I} \mid}\)个可能的频繁项集。所以可以用前缀树通过BFS或者DFS来枚举项集。

然后要完成支撑计算，这一步计算每一个候选模式\(X\)的支撑，并且判断它是否为频繁的。

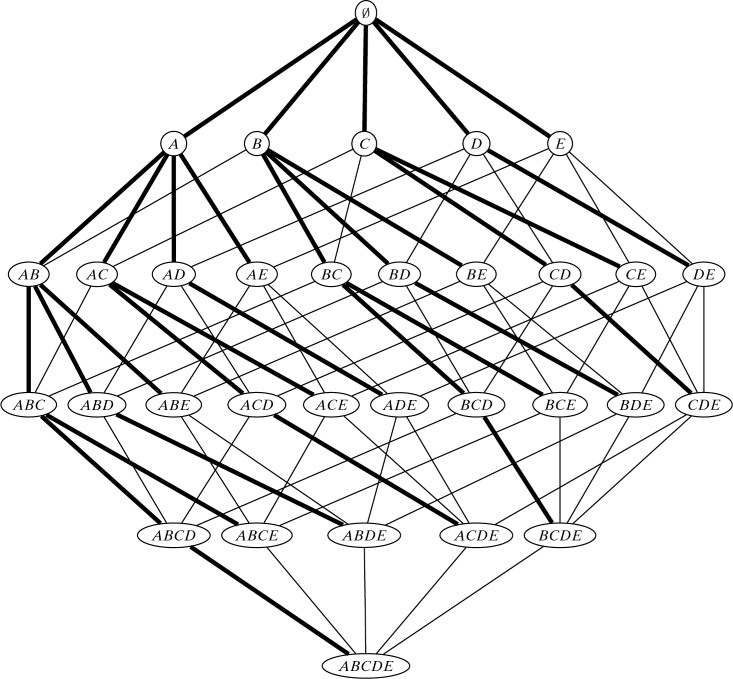
但是这种方式的计算复杂度太大，支撑的计算在最坏的情况下需要\(O(\mid \mathcal{I} \mid \cdot\mid\mathbf{D}\mid)\)的时间。由于一共有\(O(2^{\mid \mathcal{I} \mid})\)个可能的候选，暴力枚举的复杂度为\(O(\mid \mathcal{I} \mid \cdot\mid\mathbf{D}\mid\cdot 2^{\mid \mathcal{I} \mid})\)。这种复杂度在现实中是不可接受的。

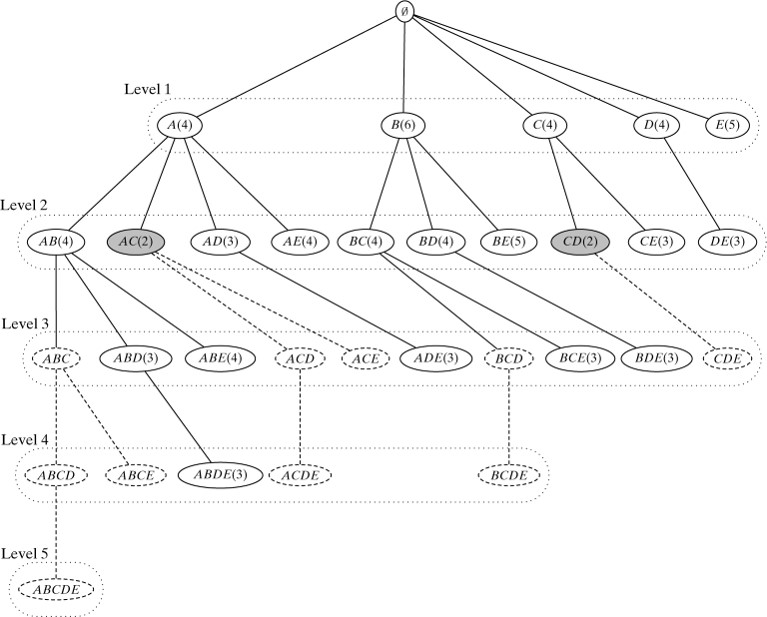
逐层的方法：Apriori算法

根据两个依据进行剪枝：

1. 若\(X\)是频繁的，则其任意子集\(Y\subseteq X\)也是频繁的
2. 若\(X\)不是频繁的，则任意超集\(Y\supseteq X\)都不是频繁的

---