Black First Won

五子棋中存在先手黑棋必赢的策略，所以职业比赛中会设置带禁手和不带禁手的区别。在没有计算机的年代里，人们只是感觉黑棋可能存在绝对的赢面，后来到1992年Victor Allis通过编程证明不带禁手的五子棋，是黑必胜的。后来在2001年Janos Wagner第一次证明带禁手的五子棋，也是黑必胜的。

m,n,k-game

在数学证明上，像五子棋这类的游戏可以归纳成一种固定的规则模式，称为m,n,k-game¹，在\(m\times n\)的棋盘上\(k\)个相同颜色的棋子相连就获胜。在最理想下法的情况下，五子棋（15，15，5）是有必胜策略的，（11，11，5）也是先手必胜的。下文为了简单起见以五子棋为例，进行必胜策略的说明。

五子棋

人们发现在五子棋的玩法中，有些常见的开局走法总是能让先手的黑棋获胜，并且总结出一些先手黑棋必胜的开局：

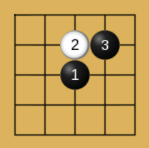
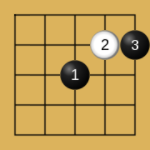
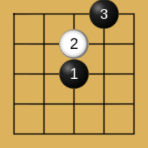
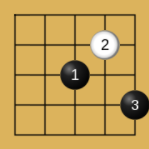
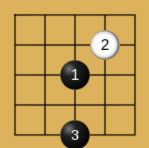
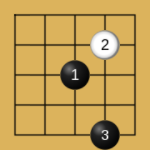
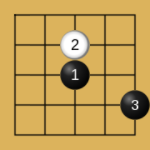
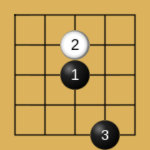
Proof Number Search

PN-Search是一种博弈树搜索算法，一个完整的博弈树²会有一个起始节点代表赛局中某一个情形，接着下一层的节点是父节点赛局下一步的各种可能性，一直扩展到游戏结束。而对于双人博弈的游戏，某一方获胜（就当是让黑手先行赢）的目标可以简化成一个与或树（And-Or-Tree）问题。

And-Or-Tree

在把大问题分解成小问题的时候，可以使用与或树表示大问题和小问题、小问题与小问题之间的关系³。把大问题分成一系列较为简单的小问题，每个子问题又可以分成若干个更加简明的子问题，重复此过程，直到不需要再分解或者不能再分解为止，把各个子问题的解复合起来就得到了原问题的解，问题的分解过程可以用一个树表示出来。

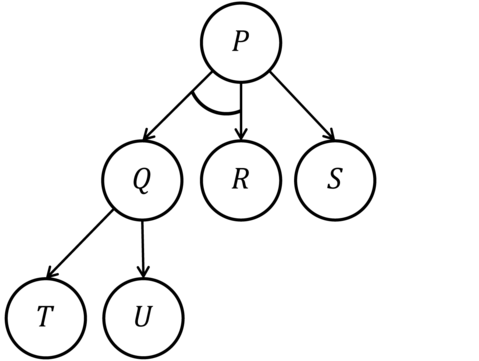
例如，问题P可以分解为Q和R，其中Q和R只有同时解出来P才可以解出来，而P也可以等价于S，只要S能解出来，P也能解出来，同理，Q也等价于T和U，只要T、U中任意一个可以解，那Q也可以解出来。上图就是一个问题P的解空间示例。

在PN-search中要尽量将节点转化为Or节点，尽量不要映射到And节点，因为在下棋这类落子博弈中，“或”节点往往对我方比较有利，我们可以有选择落子的主动权，一个被扩展的“或”节点至少有一个子节点为真，则该节点也为真。而“与”节点往往代表对方，只能被动地等待对方出招，所以要考虑最为不利的局面。因此被扩展的“与”节点中只要有一个子节点为假，则该节点也为假⁴。

Concept

如果一方玩家需要获胜则需要创造至少两个上图所示的威胁走法。在正式的游戏中，可能存在的走法非常多，解的搜索空间非常的巨大，对于内存和计算资源都有很高的要求。

Alpha-beta Search

Alpha-Beta剪枝是一种搜索算法，用以极小化极大算法（Minimax算法）搜索树的节点数。是一种对抗性搜索算法。主要应用于机器游玩的二人游戏（如井字棋、象棋、围棋）当算法评估出某策略的后续走法比之前策略的还差时，就会停止计算该策略的后续发展。该算法和极小化极大算法所得结论相同，但剪去了不影响最终决定的分枝。

function alphabeta(node, depth, α, β, maximizingPlayer) is
    if depth = 0 or node is a terminal node then
        return the heuristic value of node
    if maximizingPlayer then
        v := -∞
        for each child of node do
            v := max(v, alphabeta(child, depth – 1, α, β, FALSE))
            α := max(α, v)
            if β ≤ α then
                break (* β cut-off *)
        return v
    else
        v := +∞
        for each child of node do
            v := min(v, alphabeta(child, depth – 1, α, β, TRUE))
            β := min(β, v)
            if β ≤ α then
                break (* α cut-off *)
        return v

初始调用方式为

alphabeta(origin, depth, -∞, +∞, TRUE)

在五子棋类的游戏AI的设计中要尽量减少策略的搜索空间，所以也可以通过一些地毯谱⁵的方式进行辅助搜索。但是即使如此，还是需要非常大的搜索量，并且和人类专家级别的策略比起来还是有些落后。

Threat-space search

因为使用Alpha-Beta剪枝还是不尽如人意，所以再将策略限制在走威胁落子（Threats）策略里：

1. 一步威胁的获利方块是攻击者落的子
2. 一步威胁的代价方块是防御者落的子
3. 除了获利方块，一步威胁下剩下的方块都包括一种威胁可能性
4. 如果其余的威胁A的可落子方块都是威胁B的获利方块，称威胁A取决于威胁B
5. 威胁A的依赖树以A为根节点，并且只包含取决于它的子节点，每个节点J的子节点的威胁都是取决于J的
6. 如果在树P中有一个威胁A的，树Q中有一个威胁B，且A中的获利方块是B中的代价方块，则这两棵树是冲突的

所以根据以上的定义，可以将威胁空间搜索描述成下面的形式：

1. 独立于威胁B的威胁A在威胁B的搜索树中是不合法的
2. 在威胁空间搜索树种，只有用于攻击的威胁会被考虑在内，一旦一个潜在的威胁序列被发现，就会枚举所有对抗方式来看这个序列是否能站的住脚

通过设计这些算法，和通过这些算法进行验证，先手执黑在无更多对应规则的情况下确实有必胜的策略。（PS：这里还是没有讲清楚，但是我不想讲了）