自然语言处理领域中有很多模型，为了解决其中碰到的问题而提出包括词性标注、句法分析、机器翻译、信息检索等方法。

在Hinton的ANN课程中第四节给出了关于统计语言模型的内容和文献，统计模型以统计特征给出，也就是，某个词汇在大量的文章中（一个语言的资料库，包含了大量用这个语言写成的作品，比如说文学作品，日常对话，报纸新闻）都是怎样出现的，并且以怎样的结构出现的（其实就是语序吧，跟在什么类型的词语后面，并且还会跟着某种词），根据在以往的文章库中出现的频率来做可能性预测。

\begin{equation} \hat{P}(w^T_1) = \prod_{t=1}^T \hat{P}(w_{t}|w^{t-1}_1) \end{equation}

其中，\(w_t\) 是序列 \(w_i^j\) 中的第t个词，\(w^j_i=(w_i,w_{i+1},...,w_j)\) , \(\hat{P} (w_t\vert w^{t-1}_1)\) 可以用\(\hat{P}(w_t\vert w^{t-n+1}_{t-1})\)来近似，也就是n-gram语言模型。

构造（训练）N-gram语言模型，在训练预料库中统计获得n-gram的频度信息。

• 更大的n：对下一个词出现的约束性信息更多，更大的辨识力
• 更小的n：在训练语料库中出现的次数更多，更可靠的统计结果，更高的可能性。

为了能够给出以后计算所需要的参数要构建词表： 给出在词表个数为 \(\vert V\vert =20000\) 词的情况

n	所有可能的n-gram的个数
2(bigrams)	\(20000^2=400000000\)
3(trigrams)	\(20000^3=8000000000000\)
4(4-grams)	\(1.6\times10^{17}\)

这种计算量是过于庞大,计算方式通常为： \begin{equation} P(S)=p(w_1)P(w_2|w_1)p(w_3|w_1w_2)…p(w_n|w_{n-1}w_{n-1}) \end{equation} 其中，S表示的是一个字符串，里面的每一个w都表示一个单词， 这个概率的提取从语料库中取得：

\begin{equation} p(w_i|w_{i-2}w_{i-1})=\frac{C(w_{i-2}w_{i-1}w_i)}{C(w_{i-2}w_{i-1})} \end{equation}

但很现实的问题是，并不是每一种\((w_{i-2}w_{i-1}w_i)\)都是已经在语料库中出现过的，但是在测试的时候是可能出现训练中从未出现过的短语的，比如（I like cat，I like dog）这些都出现过，但是如果你碰到（I like shit）然后训练的时候这种东西是没有出现过的，那就变成0了，然后就会输出为错误，这就会使得我们的模型局限性太大了，什么也干不了。所以有改进方法见PPT

神经网络语言模型

Hinton在1985年提出distributed representation，Miikkulainen and Dyer，Xu and Rudnicky分别在1991和2000提出利用神经网络建模语言模型。

NNLM(Neural network Langauge model)的一个核心概念是词向量(Word Embedding),词向量源于Hinton在Learning distributed representations of concepts提出的Distributed Representation。

词向量

简而言之，词向量是用一个向量来表示一个词，一定程度上可以用来刻画词之间的语义距离。是一种讲符号数学化的方式，目前为止比较常用的是One-hot Representation，这种表示方式是把词表示为一个很长的向量，这个向量的大小就是词汇表的总数大小，其中只有一个1，其他均为0。比如在语料词汇库仅有8个单词时，可以这样表示其中的一个单词：

• “cat”: [0 1 0 0 0 0 0 0]
• “dog”: [0 0 1 0 0 0 0 0]

这样存储非常稀疏，但是也非常简洁，并且在配合最大熵，SVM等算法都更方便编程实现。 可是这样也会带来“词汇鸿沟”：任意两个词之间都是孤立的。光从这两个向量中看不出两个词是否有关系，哪怕是话筒和麦克这样的同义词也不能幸免于难。¹

而在DeepLearning中一般用到的词向量并不是这种0 1表示方法，而是Distributed Representation方式表示的一种低维度的实数向量，一般长成[0.792, −0.177, −0.107, 0.109, −0.542, …]这个样子，其维度一般取30,50,60,100，这类值。

词向量的贡献是解决某些问题带来的维数灾难，并且能够使得在更多的情况下让相关的或者相似的词在距离上更加接近了，但是也带来一些缺点，让某些词汇带上了其他的语义。词向量的提出在Hinton的文中给出了最初的说明，《Learning distributed representations of concepts》，这还让基于词向量设计的模型自带平滑功能。

词向量的训练

听说目前的模型都是在训练语言模型的同时顺便得到词向量。语言模型就是利用自动化的手段来看一个字符串是否是出自自然语言。当然这也用到了n-gram模型，是根据统计特征来进行识别的。

模型结构

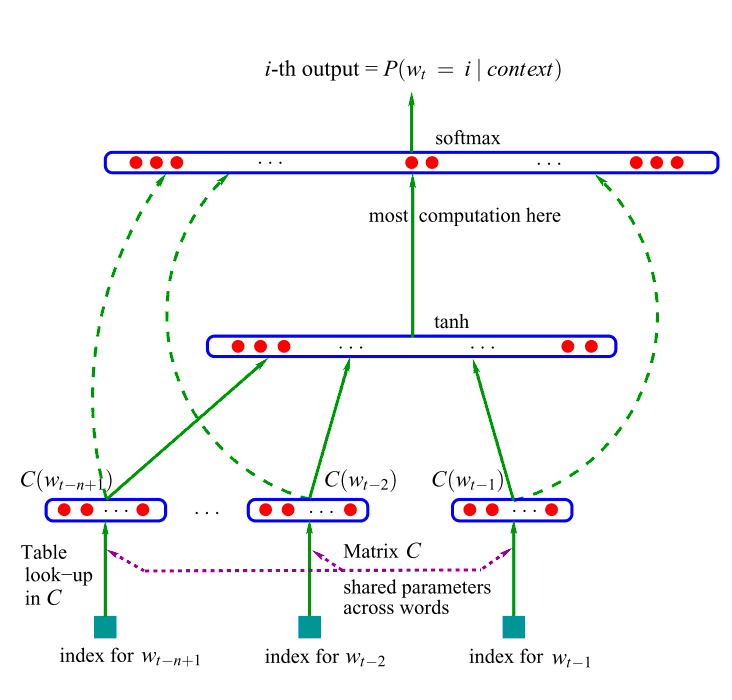
上图即为前馈神经网络。 图中最下方的 \(w_{t-n+1}, ..., w_{t-2}, w_{t-1}\) 就是前 \(n-1\) 个词。现在需要根据这已知的 \(n-1\) 个词预测下一个词 \(w_t\)。\(C(w)\) 表示词 \(w\) 所对应的词向量，整个模型中使用的是一套唯一的词向量，存在矩阵 \(C\)（一个 \(\vert V\vert \times m\) 的矩阵）中。其中 \(\vert V\vert\) 表示词表的大小（语料中的总词数），\(m\) 表示词向量的维度。\(w\) 到 \(C(w)\) 的转化就是从矩阵中取出一行。

网络的第一层（输入层）是将 \(C(w_{t-n+1}), ..., C(w_{t-2}), C(w_{t-1})\) 这 \(n-1\) 个向量首尾相接拼起来，形成一个 \((n-1)m\) 维的向量，下面记为 \(x\)。

网络的第二层（隐藏层）就如同普通的神经网络，直接使用 \(d+Hx\) 计算得到。\(d\) 是一个偏置项。在此之后，使用 \(\tanh\) 作为激活函数。

网络的第三层（输出层）一共有 \(\vert V\vert\) 个节点，每个节点 \(y_i\) 表示 下一个词为 \(i\) 的未归一化 log 概率。最后使用 softmax 激活函数将输出值 \(y\) 归一化成概率。最终，\(y\) 的计算公式为：

\begin{equation} y = b + Wx + U\tanh(d+Hx) \end{equation}

---