MuLTI

Latent Processes Identification From Multi-View Time Series

Abstract

Understanding the dynamics of time series data typically requires identifying the unique latent factors for data generation, a.k.a., latent processes identification. Driven by the independent assumption, existing works have made great progress in handling single-view data. However, it is a nontrivial problem that extends them to multi-view time series data because of two main challenges: (i) the complex data structure, such as temporal dependency, can result in violation of the independent assumption; (ii) the factors from different views are generally overlapped and are hard to be aggregated to a complete set. In this work, we propose a novel framework MuLTI that employs the contrastive learning technique to invert the data generative process for enhanced identifiability. Additionally, MuLTI integrates a permutation mechanism that merges corresponding overlapped variables by the establishment of an optimal transport formula. Extensive experimental results on synthetic and real-world datasets demonstrate the superiority of our method in recovering identifiable latent variables on multi-view time series.

Motivation

\[\begin{equation} \boldsymbol{z}_{i,t}=f_{i}(\boldsymbol{Pa}(z_{i,t}), \epsilon_{i,t}) \end{equation}\]

where $\textbf{Pa}(z_{i,t})$ denotes causal parents of $i$-th factor at current step $t$, $\epsilon_{i,t}$ denotes a noise component of causal transition. While $\boldsymbol{z}_t$ contains a complete set of latent factors that we are truly interested in, we note that each observed view may be dependent on only a subset of it. Formally, we have the following data-generating process,

\[\begin{equation} \boldsymbol{x}^{1}_{t} = g^{1}(\boldsymbol{z}^{1}_{t}), \quad \boldsymbol{x}^{2}_{t} = g^{2}(\boldsymbol{z}^{2}_{t}), \quad \text{where}~~\boldsymbol{z}_{t} = \boldsymbol{z}^{1}_{t}\cup \boldsymbol{z}^{2}_{t}, \end{equation}\]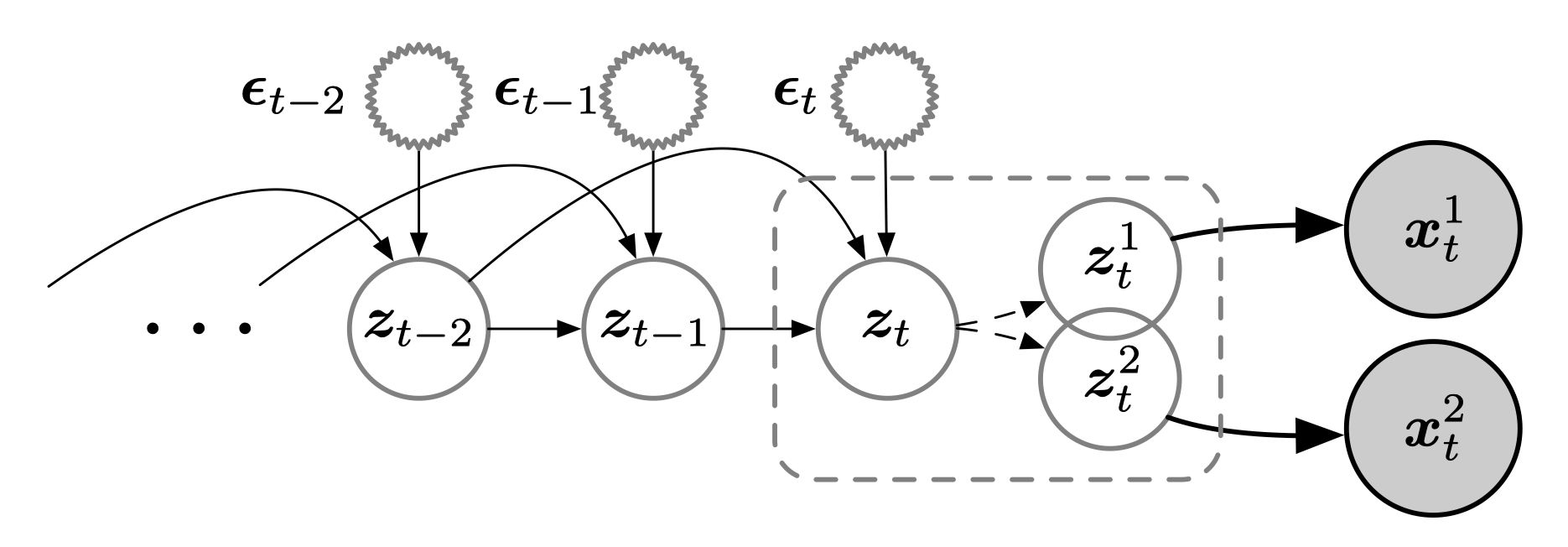

Contrastive Module

Why use contrastive learning?

Because we want make $p(\tilde{\boldsymbol{z}}_{t}, \boldsymbol{z}_{H_{t}})$ as close as possible to the ground truth $p(\boldsymbol{z}_{t},\boldsymbol{z}_{H_{t}})$, while contrastive learning can minimize the cross entropy between the two distributions.

\[\begin{equation} \begin{split} &\mathcal{L}_{\rm contr}(r,f;\mu,M):= \label{eq:loss_contr}\\ &\underset{\substack{(\boldsymbol{x}, \tilde{\boldsymbol{x}}) \sim p_{\text {pos}} \\\left\{\boldsymbol{x}_{i}^{-}\right\}_{i=1}^{M} \stackrel{\text { i.i.d. }}{\sim} p_{\text {data }}}}{\mathbb{E}}\left[-\log \frac{e^{-\delta(\boldsymbol{z},\tilde{\boldsymbol{z}}) / \mu}}{e^{-\delta(\boldsymbol{z},\tilde{\boldsymbol{z}}) / \mu}+\sum_{i=1}^{M} e^{-\delta(\boldsymbol{z},\boldsymbol{z}^{-}) / \mu}}\right], \end{split} \end{equation}\]

where $\delta(\boldsymbol{z},\tilde{\boldsymbol{z}})$ is the distance between two latent factors, $\mu$ is the temperature parameter, and $\mathcal{L}_{\rm contr}$ is the loss function for contrastive learning.

Permutation

Assume there is a common source $\boldsymbol{c}_{t}\in \mathbb{R}^{d_{c}}$ shared across all views, we can identify the components of this source by exhausting the permuation corresponding to each view.

$$ \boldsymbol{B}=\theta_{1}\boldsymbol{P}_{1}+\theta_{2}\boldsymbol{P}_{2}+\dots+\theta_{M}\boldsymbol{P}_{M}, $$

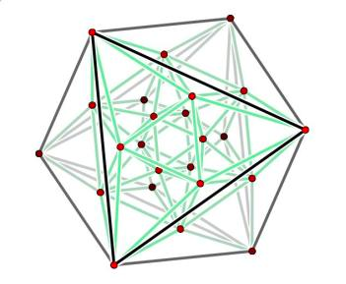
where $$\boldsymbol{P}_i$$ is the permutation matrix, and $$\theta_{i}$$ is the corresponding weight for the permutation matrix. Once the loss function is minimized, there solution converge to a unique permutation matrix, i.e., a vetex of the Birkhoff polytope.

Framework

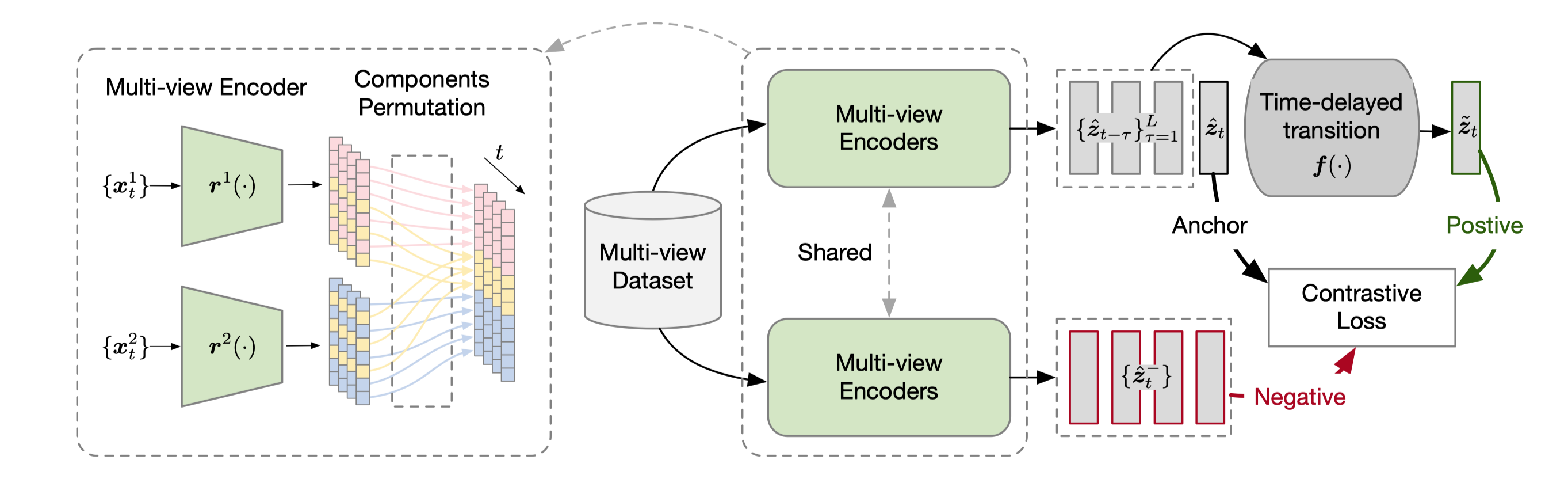
Illustration of our MuLTI framework. On one hand, we recover the view-specific latent factors $$\boldsymbol{z}^v_t$$ from individual views, which are then merged to obtain $$\boldsymbol{z}_t$$. On the other hand, we exploit the temporal dependency to obtain a causal transited latent factor $$\tilde{\boldsymbol{z}}_{t}$$ from previously estimated $$\hat{\boldsymbol{z}}_{t}$$. Thereafter, we regard them as positive pairs to optimize the contrastive loss, which serves as a surrogate of mutual information maximization to achieve identifiability.

Experiments

Multi-view vector auto-regression

Identifiability results on the VAR process $$(d = 10, L = 2)$$. Mean+standard deviation over 5 random seeds.