DRDA

Discriminative Radial Domain Adaptation

Abstract

Domain adaptation methods reduce domain shift typically by learning domain-invariant features. Most existing methods are built on distribution matching, e.g., adversarial domain adaptation, which tends to corrupt feature discriminability. In this paper, we propose Discriminative Radial Domain Adaptation (DRDA) which bridges source and target domains via a shared radial structure. It’s motivated by the observation that as the model is trained to be progressively discriminative, features of different categories expand outwards in different directions, forming a radial structure. We show that transferring such an inherently discriminative structure would enable to enhance feature transferability and discriminability simultaneously. Specifically, we represent each domain with a global anchor and each category a local anchor to form a radial structure and reduce domain shift via structure matching. It consists of two parts, namely isometric transformation to align the structure globally and local refinement to match each category. To enhance the discriminability of the structure, we further encourage samples to cluster close to the corresponding local anchors based on optimal-transport assignment. Extensively experimenting on multiple benchmarks, our method is shown to consistently outperforms state-of-the-art approaches on varied tasks, including the typical unsupervised domain adaptation, multi-source domain adaptation, domainagnostic learning, and domain generalization.

Motivation

Feature Discriminability

When using the linear classifier formulation, the likelihood of \(i\)-th sample belonging to \(k\)-th category is:

\[\begin{equation} p_{ik}\propto \exp(\boldsymbol{W}^{\top}_{k}\boldsymbol{z}_{i}+b) \end{equation}\]

which means that the feature of each category expands outwards in different directions:

\[\begin{equation} p_{ik}\propto \exp(\|\boldsymbol{W}_{k}\| \|\boldsymbol{z}_{i}\|\cos(\boldsymbol{W}_{k}, \boldsymbol{z}_{i})+b) \end{equation}\]

thereby, for enhancing the discriminability of the feature, model is trained to be progressively expand the feature of each category outwards in different directions:

Hereafter, a radial structure is formed, which is inherently discriminative.

We can naturally model the latent sketches of the two domain by just using their corresponding domain centroids and category centroids.

Radial Expansion

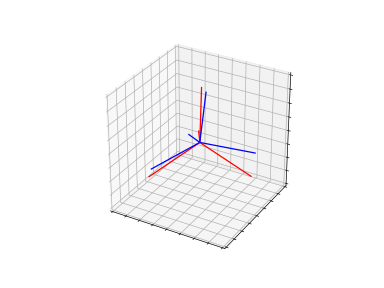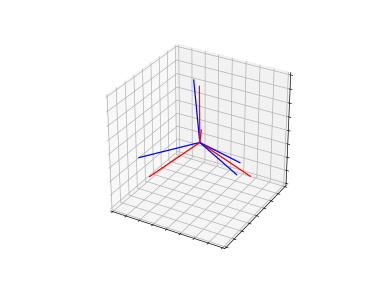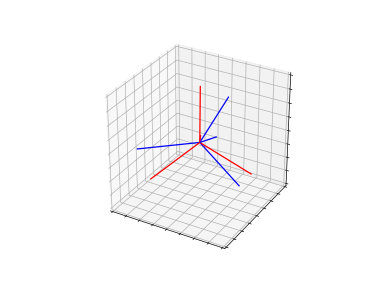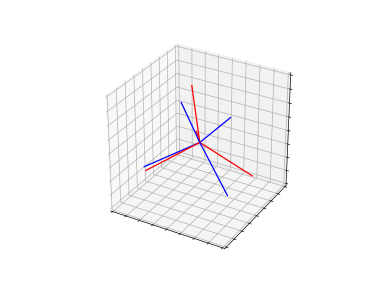
GWD adaptation

Global Alignment

Consider there is a global transformation \(\mathcal{T}(\cdot): \mathcal{V} \mapsto \mathcal{V}\).

Local Finetune

Consider the follow shapes, which have different details. More details about the optimal transport can be found in optimal transport and Gromov-Wasserstein Distance:

\[\begin{equation} GW^{2}_{2}(c_{s}, c_{t}, \mu, \nu) = \min_{\pi \in \Pi(\mathcal{V}^{s},\mathcal{V}^{t})} J(c_{s}, c_{t}, \pi) \end{equation}\]

where

\[\begin{equation} J(c_{s}, c_{t}, \pi) = \sum_{i,j,k,l}|c_{s}(\boldsymbol{v}^{s}_{i}, \boldsymbol{v}^{s}_{j})-c_{t}(\boldsymbol{v}^{t}_{k}, \boldsymbol{v}^{t}_{l})|\pi_{i,j}\pi_{k,l} \end{equation}\]

By minimizing the Gromov-Wasserstein distance, we can finetnue the two shapes to be similar.

Please see the paper for details.

DRDA

The DRDA framework is a straightforward extension to Nerfies. The key difference is that the template NeRF is conditioned on additional higher-dimensional coordinates, where the higher dimensional coordinates are given by an “ambient slicing surface” which can be thought of as a higher dimensional analog to the deformation field.

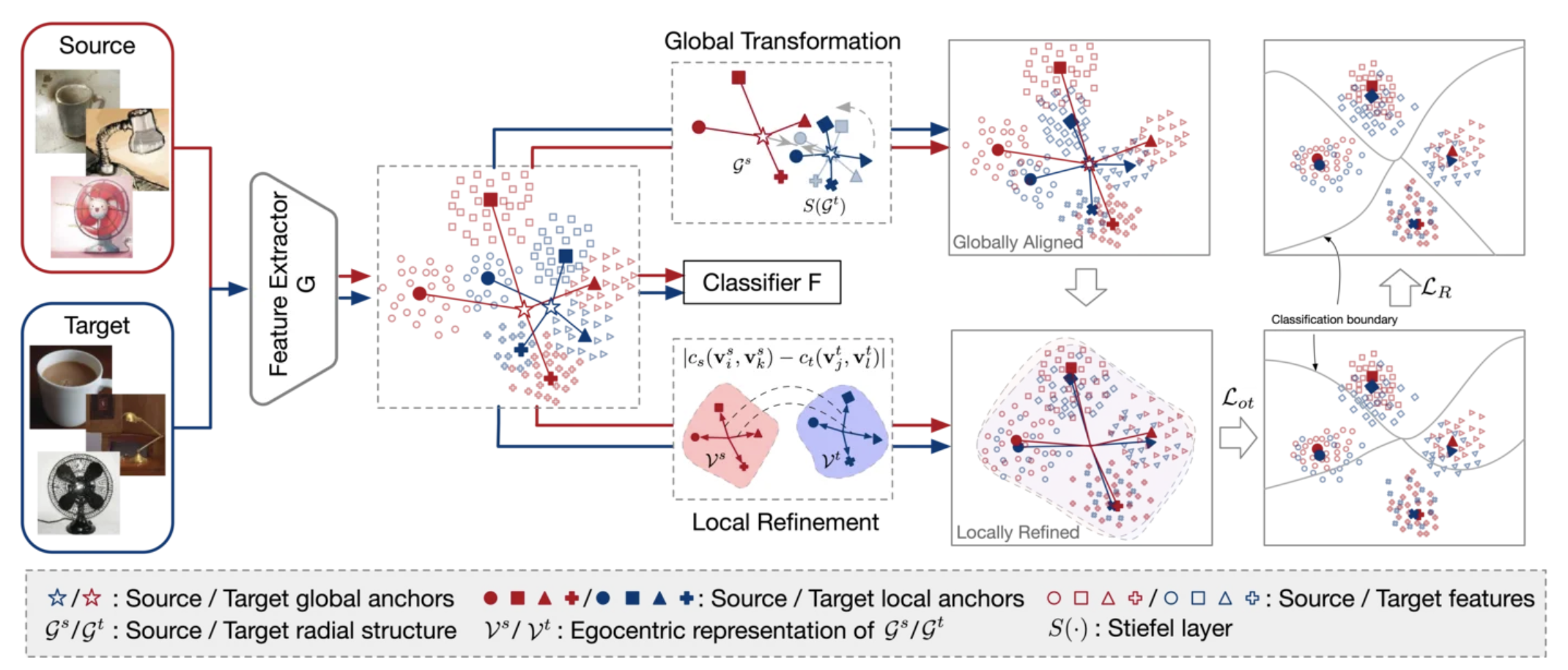
DRDA handles domain shifts by modeling a low-dimensional structure in high-dimensional space, thereby producing more reliable alignment on the different domains. (rotate and translate the target structure to align the source structure)

To give a intuitive illustration of the feature evolution during model training, we built a simplified LetNet while reducing the bottleneck dimension to 2 and training it with the task MNIST→USPS.

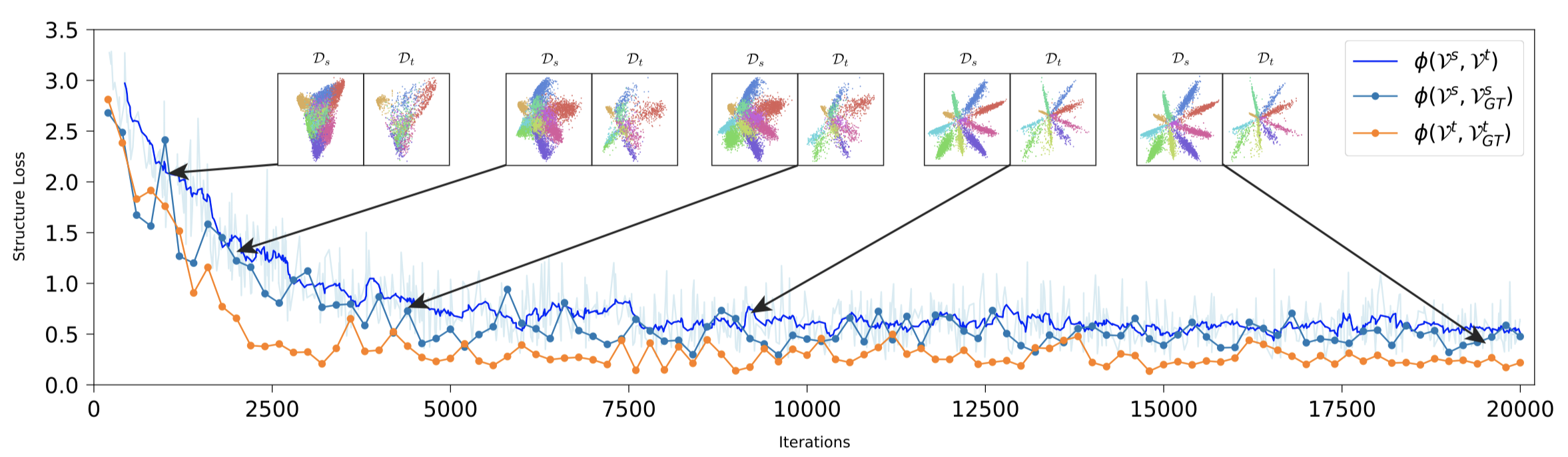
Feature Evolution

Acknowledgements

Special thanks to Weijie Liu and Changjian Shui for their constructive suggestions.