MST-Analysis | Curiousity Hub

蛋白质或者小分子在生物液体（例如血清或细胞裂解物）中会发生相互作用，可以把这种作用想象成你穿着毛衣经过长满苍耳的灌木丛时，那些满是钩子的种子粘的你满身都是，但是如果你穿的是冲锋衣，那么可能就一颗也粘不上。这些分子化合物之间也是如此，它们之间有选择性地相互结合。了解这些结合的亲和度是研发新药的关键参考。

把一堆宏观上看不到的蛋白质放入纤细透光的毛细管中，再加热到适合的温度（差不多是人的体温，因为这些小东西对于温度很挑剔），就可能看到在这种自由、接近人体内环境的场景中，分子会相互结合。如果它们相互结合了，那么对光的折射反射率就不同了，所以在宏观上用荧光强度就可以从侧面反映它们结合的强度 ¹。另外，两种分子之间的结合比例到底是多少也是一个关键问题，所以需要配比不同的浓度梯度的样品都测测看。

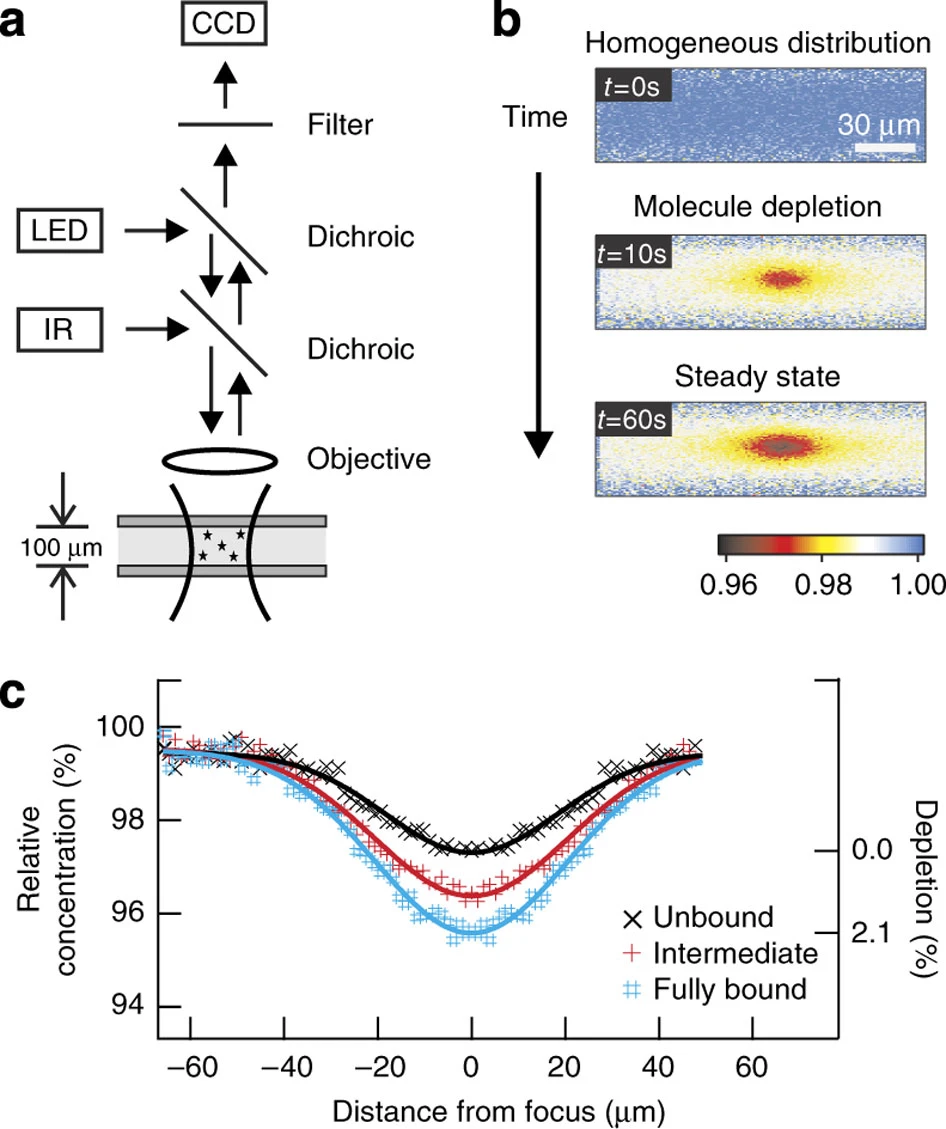
a. 观测这个微观过程的设备结构，b. 刚开始因为温度不合适，分子之间不结合，加热之后它们就快速行动起来，并呈现出宏观的变化，c. 从侧面的荧光强度曲线可以观测到它们的结合强度

理论背景

当溶液加热时，分子就会沿着温度梯度移动（详见热致扩散），移动方向和质量扩散方向相反。这两种相反的浓度变化趋势会形成一种平衡：

\begin{equation} \frac{c}{c_{0}}=\exp[-S_{T} \cdot(T-T_{0})] \end{equation}

这里的相对浓度取决于Soret系数\(S_{T}\)和温度梯度\(\Delta T=T-T_{0}\)，其中，Soret系数的确定还需要考虑很多物理现象，包括表面参数（电荷、疏水性）、缓冲液中离子移动产生的电场等。不过，这里直接给他套个简单模型差也差不多了：

\begin{equation} S_{T}=\frac{A}{kT}\left( -\Delta s_{\rm hyd}(T)+\frac{\beta \sigma^{2}_{\rm eff}}{4\varepsilon \varepsilon_{0}T} \cdot \lambda_{\rm DH} \right) \end{equation}

\(A\)是分子的表面积，\(\sigma_{\rm eff}\)表示有效电荷，\(\Delta s_{\rm hyd}\)表示分子-溶液界面的水合熵，\(\lambda_{\rm DH}\)表示德拜-休克尔筛分长度，\(\varepsilon\)表示介电常数，\(\beta\)表示其温度导数。

当蛋白质和分子相互作用时，表面积\(A\)会改变，\(\Delta s_{\rm hyd}\)水合熵会变，有效电荷\(\sigma_{\rm eff}\)也会变。即一点点微小的构型改变，我们都可以通过宏观的统计数据（例如浓度）捕捉到。

所以，基于物质作用定律可以推导出如下的经验公式：

\begin{equation} \frac{BL}{B_{0}}=\frac{(L_{0}+B_{0}+K_{d})-\sqrt{(L_{0}+B_{0}+K_{d})^{2}-4L_{0}B_{0}}}{2B_{0}} \end{equation}

这里 \(B\) 是指结合位点，\(L\)是指配体，\(BL\)是它们形成的复合物的浓度。\(L_{0}\)表示每个数据点添加配体的量，\(B_{0}\)是指结合状态对应的总浓度。\(K_{d}\)是解离常数，它量化了配体与特定受体之间的亲和程度。

基于一种线性变化的思路，你的配体浓度低了，那么溶液中只有部分受体处于结合状态，你只有滴滴滴滴到差不多过量了以后，才能保证所有的受体都和配体结合了。那么那个就是饱和浓度，但是我们刚开始怎么会知道那东西是多少，所以你就得用各种浓度梯度去试出来。这样，我们就可以写出一条随浓度连续变换的插值关系来：

\begin{equation} \Delta c_{\rm measured}=f\cdot \Delta c_{\rm bound}+(1-f)\cdot \Delta c_{\rm unbound} \end{equation}

数据分析

前面已经说了，浓度是怎么变，荧光强度就怎么变，所以用荧光强度值\(F\)代入就有：

\begin{equation} F=(1-f(c))F_{\rm unbound} + f(c)F_{\rm bound} \end{equation}

注意：这里的 \(F_{\rm unbound}\)和\(F_{\rm bound}\)是不知道的，只能按照下面这个公式去代入数值去估计：

\begin{equation} f(c)=\frac{c+c_T+K_d-\sqrt{\left(c+c_{T} + K_d\right)^2+4 c c_T}}{2 c_T} \end{equation}

以上带入的参数都应该首先进行归一化，\(\Delta c_{\rm measured}\)就对应于\(\frac{BL}{B_{0}}\)，也对应于归一化的荧光强度 \(F_{\rm norm}\)。其中，荧光的强度的归一化一般遵照一条约定俗成的规则如下图所示：

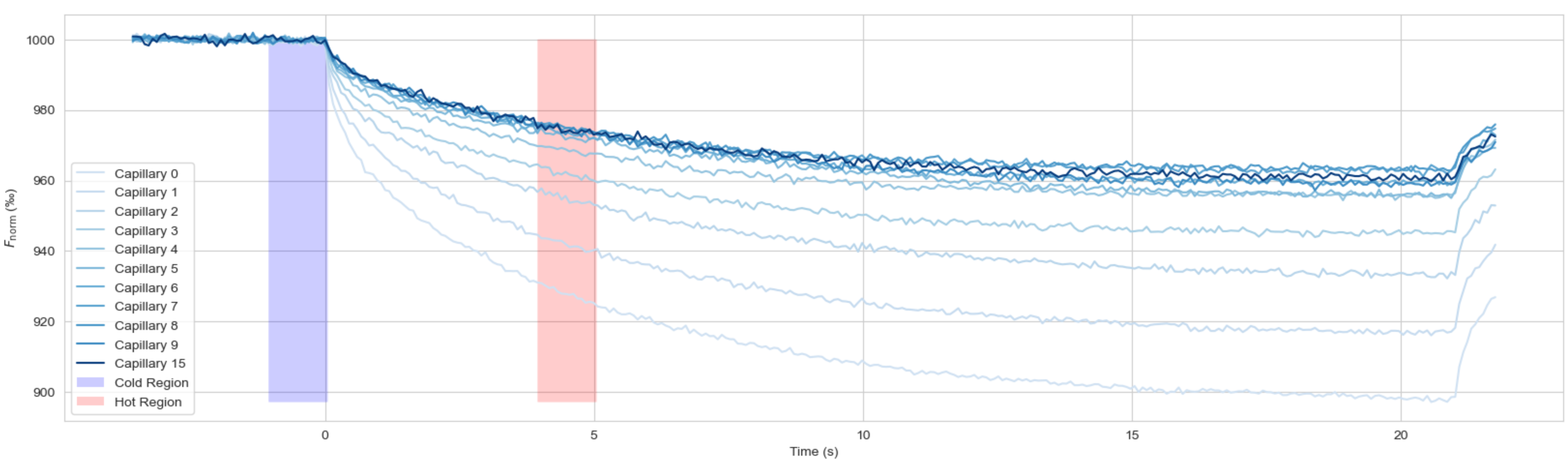
蓝色区域一般作为归一化常数\(F_{0}\)，对应于加热前荧光强度，红色区域作为被归一化荧光强度\(F_{1}\)。之所以这么选择是因为：在红外激光加热几秒钟后，即使扩散缓慢且在测量时间内没有达到稳态，浓度曲线通常在几秒钟后即可区分。要的就是这种区分度，所以在一般情况下取其第4秒到第5秒这一秒内的荧光强度样本点就可以了，这只是一种习惯。每个箱线图都对应于一组一秒内的荧光强度，绝对数值不那么重要，数值随配体的浓度变化规律才重要。

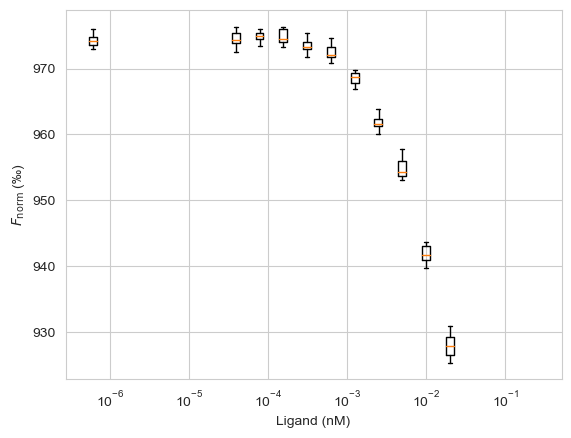
Python 拟合

首先导入必要的库，一般仪器导出的 .moc 文件就是个 SQLite 文件，已经有雷锋写好了解码函数²可以用于解码，导入这个 MSTProcess 即可：

import numpy as np
import MSTProcess as MST
from scipy.optimize import curve_fit, minimize

# 导入MST实验数据
MOCfile = MST.openMOCFile('../data/xxxx.moc')

然后定义结合比例公式：

def K_d_model(c, K_d, F_unbound, F_bound, c_T):
    def func(c, K_d):
        # Protein-binding assays in biological liquids using microscale thermophoresis
        val = (c + c_T + K_d - np.sqrt((c + c_T + K_d) ** 2 - 4 * c * c_T)) / (2 * c_T)
        return val
    return (1 - func(c, K_d)) * F_unbound + func(c, K_d) * F_bound

接着定义模型拟合的损失函数：

def robust_loss(params, c_T, c, y_data):
    K_d, F_unbound, F_bound = params
    predictions = K_d_model(c, K_d, F_unbound, F_bound, c_T)
    residuals = predictions - y_data
    loss = np.sum(2 * (np.sqrt(1 + (residuals ** 2))) - 2)
    # loss = np.sum(residuals ** 2)
    return loss

然后进行拟合：

# 浓度序列
x_data = concentr_list
# 归一化后的荧光强度序列
y_data = np.asarray(F1_list.mean(axis=1))
# 初始的猜测值 [K_d, F_unbound, F_bound] 用于帮助更快求解
init_params = [0.1, 974, 929]
res = minimize(robust_loss, init_params, args=(c_T, x_data, y_data))
# 打印拟合结果
print(f"K_d: {res.x[0]}, F_unbound: {res.x[1]}, F_bound: {res.x[2]}")

完整实现代码参见：https://github.com/lion-forest/MST-anaylysis

名词解释³

热致扩散，Thermaldiffusivity：质扩散和热传导耦合引起的热质扩散，常称之为索瑞效应和杜伏效应。在热质扩散中，由于温度梯度引起混合物中出现附加的浓度梯度而造成传质，是于1893年由索瑞（C. Soret）在液体中发现的。杜伏效应则是指由于各种物质互相扩散引起温度梯度，或者说，由于有浓度梯度引起温度梯度，这是杜伏（L. Dufour）于1872年在气体中发现的。杜伏效应是索瑞效应的逆效应。
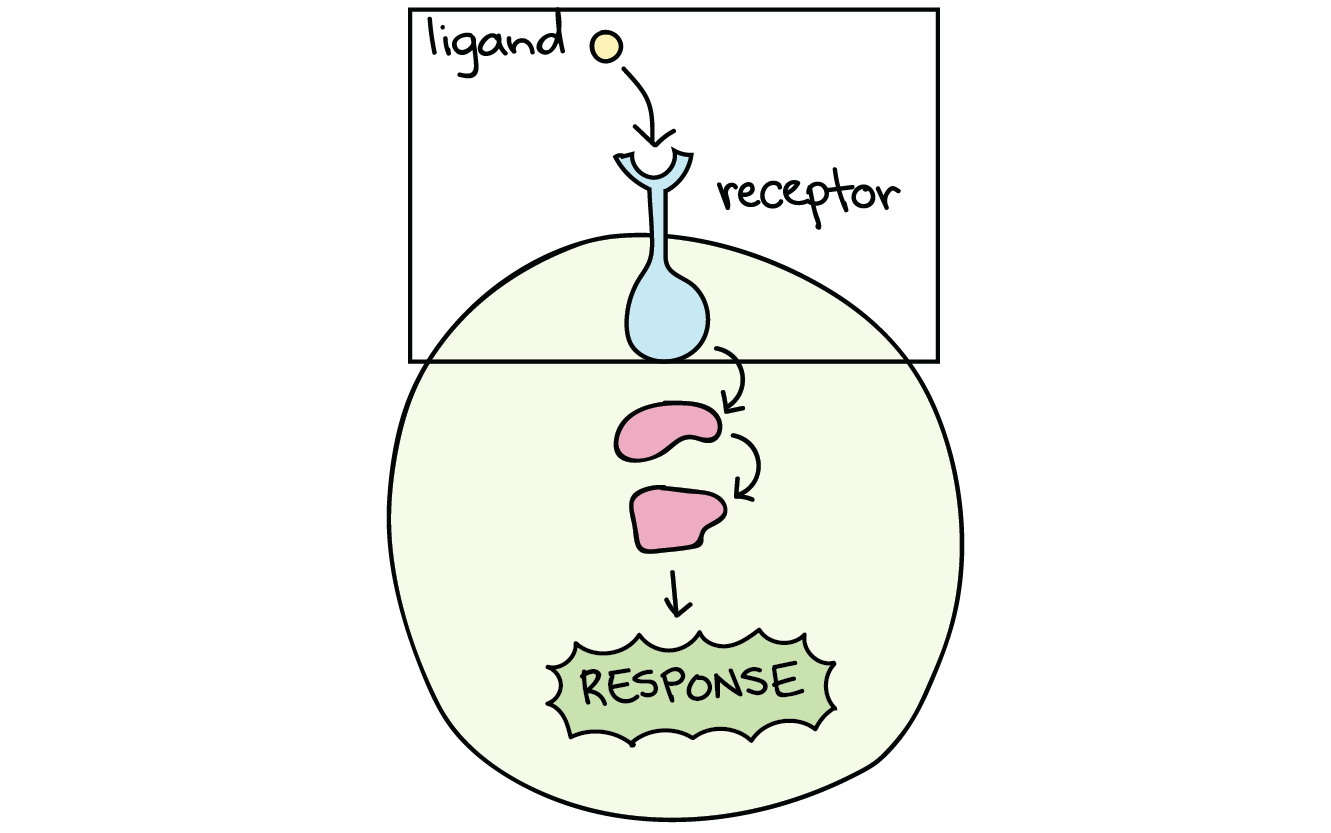
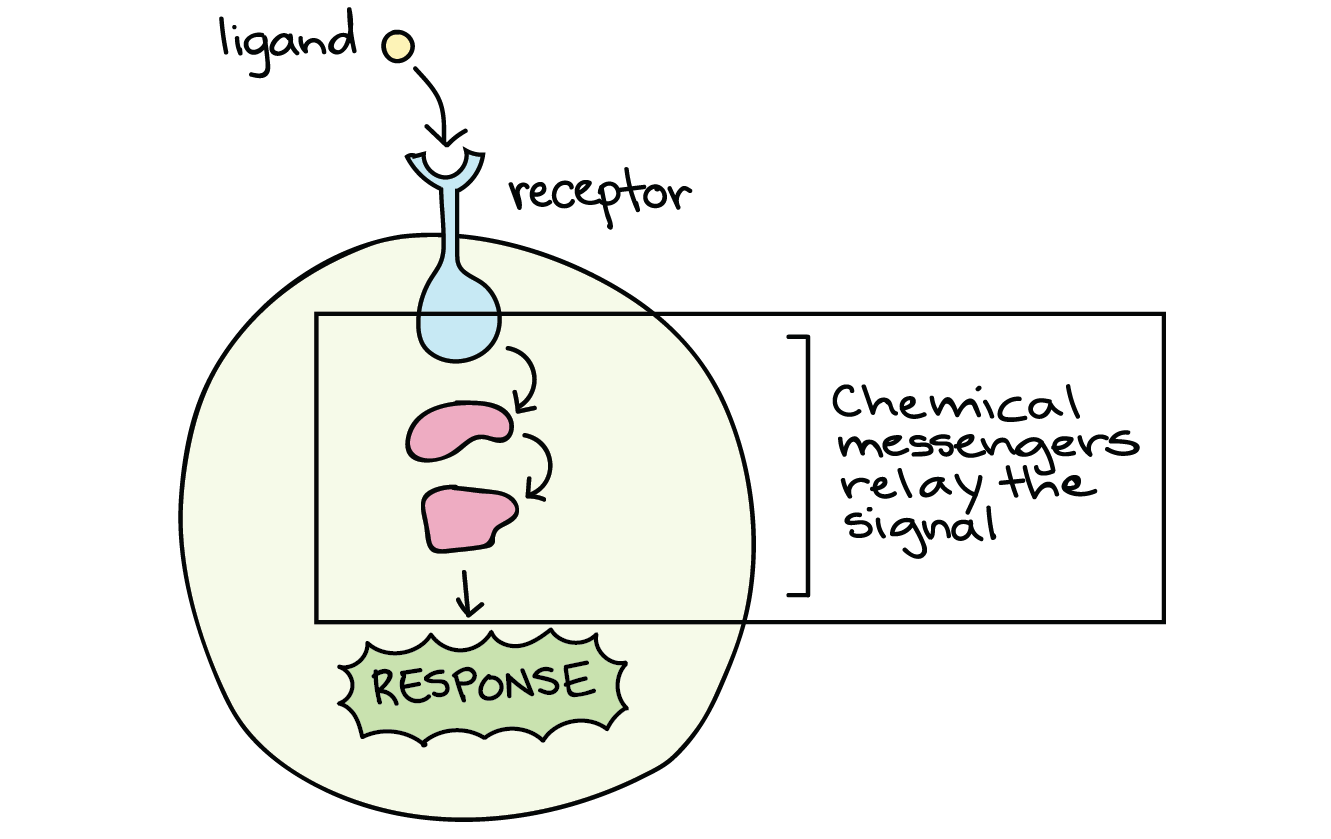
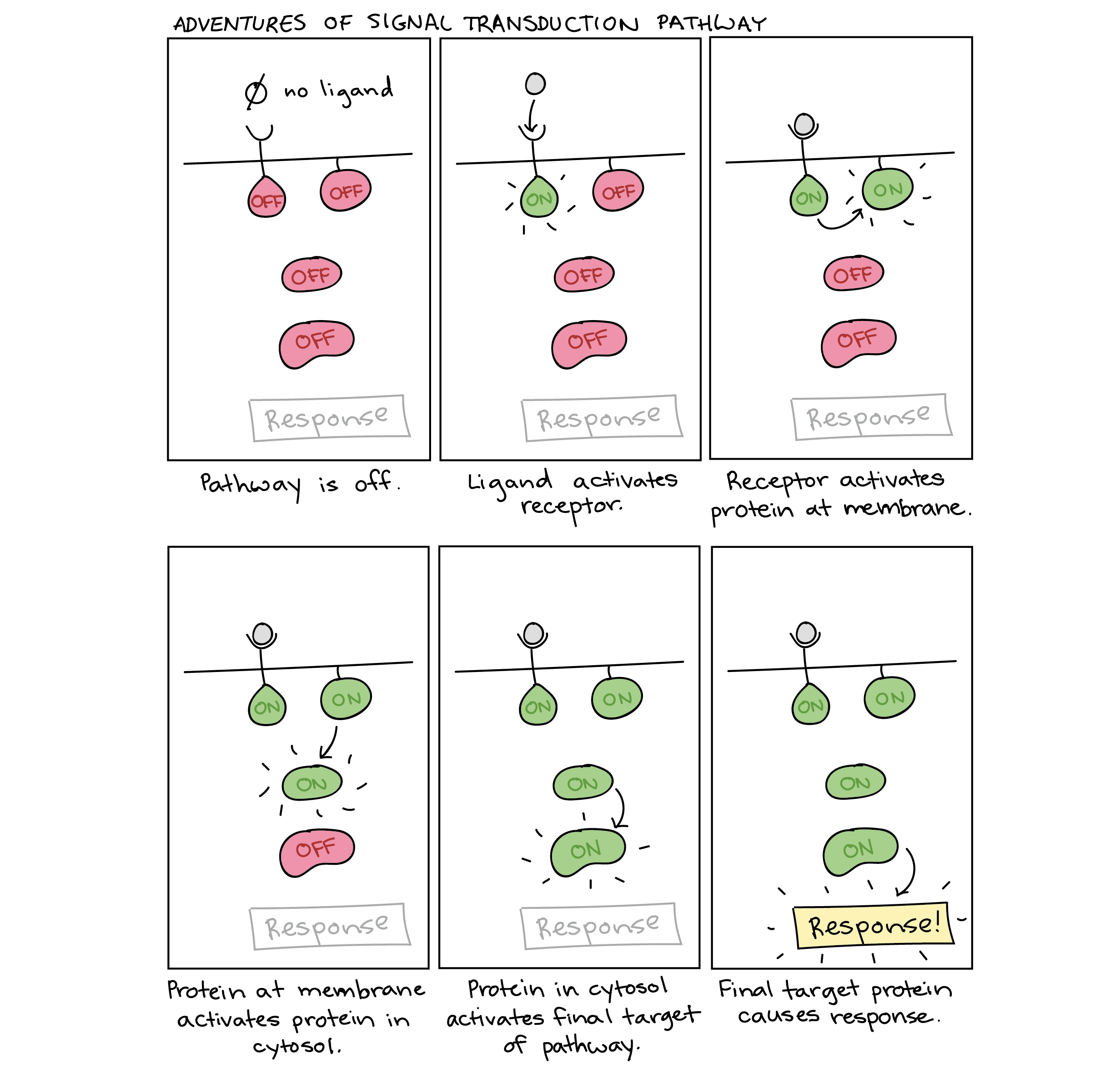
受体（Receptor）：指一类能传导细胞外信号，并在细胞内产生特定效应的分子。包括膜受体和胞内受体。
配体（Ligand）：指一种能与受体结合以产生某种生理效果的物质。细胞外能与受体结合的分子一般称之为配体，包括激素生长因子，细胞因子，神经递质，还有其他各种各样的小分子化合物