最优传输理论

最优传输问题的描述，如果用两个沙堆的问题表示：一个沙堆如何通过最小的代价推成和另一个沙堆一样的形状。或者另外一个电商的问题：电商有 \(N\) 个储存区域，同时 \(M\) 个订购电子书阅读器的客户。假设第 \(n\) 个存储区域 \(x_n\) 有 \(m_n\) 个阅读器，第 \(k\) 个客户 \(y_k\) 订购 \(h_k\) 个阅读器。传输代价 \(c(x,y)\) 是存储区域 \(y\) 与客户 \(x\) 之间的距离。最优传输问题就是要找到最合适的方式，将存储区域中的所有阅读器运送到订购它们的客户那里。传输地图 \(\Pi\) 可以视为一个矩阵，矩阵的条目或元素 \(\Pi_{nk}\) 表示从第 \(n\) 个存储区域发送到第 \(k\) 个客户的电子阅读器数量。为了保持一致，离开第 \(n\) 个存储区域的所有阅读器总数必须等于在该区域中存储的阅读器总数，同时所有顾客收到的阅读器总和必须等于顾客订购的电子书阅读器的数量¹。

问题形式化

传输地图的形式有一个确定的约束，也就是两个分布中的元素数量都是固定的传输的东西不会超过某个分布本身有的数量之和。 \begin{equation} \begin{array}{c}{\sum_{k} \Pi_{n k}=m_{n}} \\ {\sum_{n} \Pi_{n k}=h_{k}}\end{array} \end{equation} 另外，要服从一个约束，所有矩阵的元素必须为正的，约束下的最优解则为： \begin{equation} \hat{\gamma}=\operatorname{argmin}_{\Pi} \sum \Pi_{n k} c\left(x_{n}, y_{k}\right) \end{equation} 其中 \(\gamma\) 表示要把一个分布 \(P(X)\) 变换成另一个分布 \(Q(Y)\) 的传输方案，是传输地图 \(\Pi\) 中的一个子集，这个子集能够使二者之间的传输的代价最小化。虽然在现实中，一次可以运多个，运输成本和运输量不会是线性关系，但是出于分析方便下面使用这种简化的表述形式。

其中为了方面分析的过程，约定下面的符号：

• 度量空间 \(\mathcal{X}\) 和 \(\mathcal{Y}\) （完全的，可分的）
• 代价函数 \(c:\mathcal{X}\times \mathcal{Y}\rightarrow \mathbb{R}\cup \{\infty \}\) （下界，lsc）
• 概率测度 \(\mu\in \mathcal{P}(\mathcal{X})\) 和 \(\upsilon\in \mathcal{P}(\mathcal{Y})\) 或者可以写成 \(\mu=\frac{1}{N}\sum^{N}_{i=1}\delta_{x^{i}},\nu=\frac{1}{M}\sum^{M}_{i=1}\delta_{y^{i}}\) (离散的情况下可以立即成一种计数统计手段，只有两个完全一样的数据会被加两次，离散情况下很可能分布统计中的每个bin都一样高且为\(\frac{1}{N}\)或\(\frac{1}{M}\))

原始形式

• 如何用做最小的功把一堆沙子从一批坑里到另一批坑里
• 找到各个坑之间的对应关系\(T\)（传输）
• 从x搬到y做功\(c(x,y)\)，目标是让它最小化

Monge形式

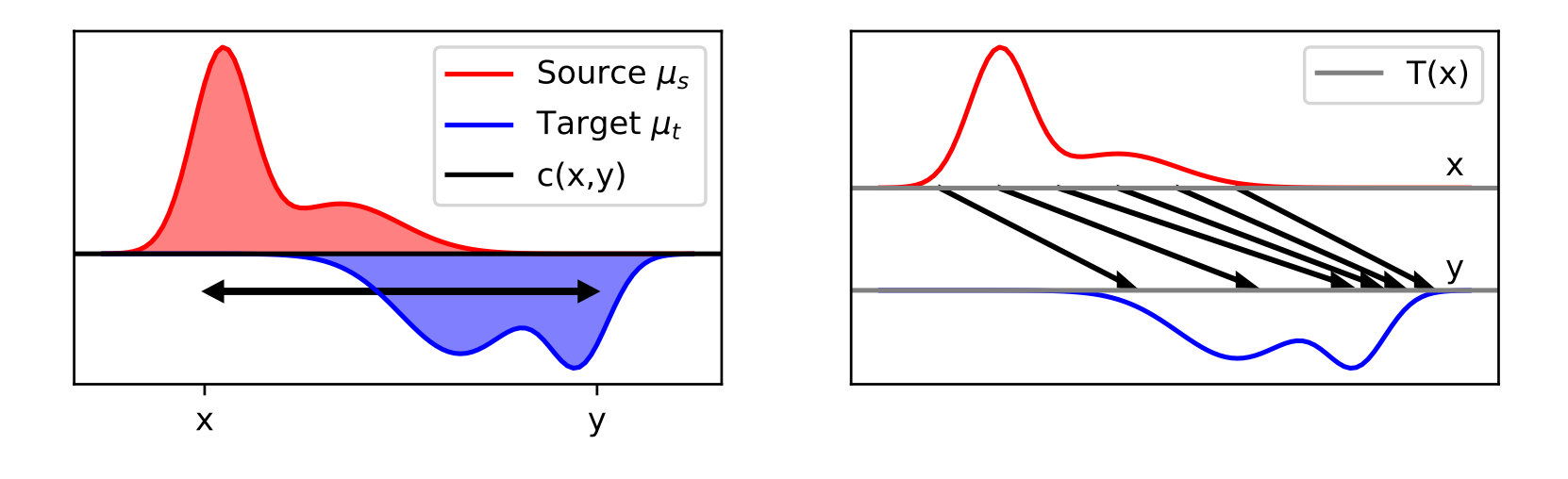
给定两个概率分布\(\mu_s,\mu_t\)和代价函数\(c:\Omega_{s}\times \Omega_{t}\rightarrow\mathbb{R}^{+}\)，Monge形式就是要找到一个代价最小的传输方案\(T\)： \begin{equation} T^{*}=\inf_{T\#\mu_{s}=\mu_{t}}\int_{\Omega_{s}}c(\mathbf{x},T(\mathbf{x}))\mu_{s}(\mathbf{x})d\mathbf{x} \end{equation} 通过把传输方案\(T\)应用到(\(\#\))某个源分布\(\mu_{s}\)上就可以把它变换成目标分布\(\mu_{t}\)。使代价综合最小的方案就是我们要的最优传输方案。

如上图所示随便取一个源分布中的子集（粗糙的说是某块区域，严格的说是任意Borel集），就可以通过传输方案映射（\(T\#\)）到目标域中去。

但是因为有这个\(T\#\mu_{s}=\mu_{t}\)限制条件的存在，这就变成了一个难以求解的非凸问题。总结成下面几点使我们不得再寻找更好的形式化：

• \(T\#\mu_{s}=\mu_{t}\) 是非凸的约束
• 最优传输方案\(T\)并不一定存在
• 最优传输方案\(T\)并不一定是唯一的
  • [Brenier, 1991]证明了当\(c(x,y)=\| x-y\| ^{2}\)时最优传输方案存在且唯一

Kantorovich 形式

为了和蒙日形式的最优传输方案做符号区分，这里的传输方案用\(\gamma\)来表示。

Kantorovich提出不一定要按照整数的方式去传输，可以把大石子打碎了传输，所以提出用两个集合耦合的概率分布来表示传输方案：

\[\begin{split} \gamma_{0}=&\text{argmin}_{\gamma}\int_{\Omega_{s}\times\Omega{t}}c(\mathbf{x},\mathbf{y})\gamma(\mathbf{x},\mathbf{y})d\mathbf{x}d\mathbf{y},\\\\ \text{s.t.}&\quad \gamma\in\mathcal{P}\{\gamma\geq0, \int_{\Omega_{t}}\gamma(\mathbf{x},\mathbf{y})d\mathbf{y}=\mu_{s},\int_{\Omega_{s}}\gamma(\mathbf{x},\mathbf{y})d\mathbf{x}=\mu_{t}\}\end{split}\]

• \(\gamma\)是\(\mu_{s},\mu_{t}\)的联合分布
• 线形规划总是会有一个解

在对最优传输的求解和相关理论证明推广的过程中，对偶理论是一项非常重要的基础理论。

Kantorovich 对偶：Let \(\mu\in\mathcal{P}(X),\nu\in\mathcal{P}(Y)\) where \(X,Y\) are Polish spaces. Let \(c:X\times Y\rightarrow [0, +\infty]\) be a lower semi-continuous cost function. Define \(\mathbb{K}\) as (given \(\mu\in\mathcal{P}(X)\) and \(\nu\in\mathcal{P}(Y)\) then \(\mathbb{K}(\pi)=\int_{X\times Y}c(x,y)d\pi(x,y)\)) and \(\mathbb{J}\) by: \begin{equation} \mathbb{J}:L^{1}(\mu)\times L^{1}(\nu)\rightarrow \mathbb{R}, \quad \mathbb{J}(\varphi, \psi)=\int_{X}\varphi d\mu+\int_{Y}\psi d\nu. \end{equation} Let \(\Phi_{c}\) be defined by: \begin{equation} \Phi_{c}={(\varphi, \psi)\in L^{1}(\mu)\times L^{1}(\nu): \varphi(x)+\psi(y)\leq c(x,y)}, \end{equation} where the inequality is understood to hold for \(\mu-almost\) every \(x\in X\) and \(\nu-almost\) every \(y\in Y\). Then: \begin{equation} \min_{\pi\in \prod(\mu, \nu)}\mathbb{K}(\pi)=\sup_{(\varphi,\psi)\in\Phi_{c}}\mathbb{J}(\varphi, \psi). \end{equation} 我们通过运货商问题直观地证明上面的这个结论，假设我们现在有一批煤矿和一些工厂，每个煤矿的产量和每个工厂的需求量都是固定的。从煤矿\(x\)运输到工厂\(y\)的成本是\(c(x,y)\)，使成本总和最小的运输方案就是Kantorovich的最优传输方案。后来，有一个聪明的运输员来找你，说你只要付\(\varphi(x)\)用于装车，\(\psi(y)\)用于卸货。为了使你更加感兴趣，他还提出他保证装车成本\(\varphi\)和卸货成本\(\psi\)一定不会超过原来的运输方案\(c(x,y)\)，即\(\varphi(x)+\psi(y)\leq c(x,y)\)。也就是Kantorovich对偶告诉我们可以找到\(\varphi\)和\(\psi\)使得价格组成方案最多都不会超过原形式的运输方案。

借助这个直观的解释（一部分给自己运，一部分交给运货商的话）给出非正式的证明过程，令\(M=\inf_{\pi\in\prod(\mu,\nu)}\mathbb{K{(\pi)} }\)，可以观察到：

\begin{equation} M=\inf_{\pi\in \mathcal{M}_{+}(X\times Y)}\sup_{(\varphi, \psi)}\left(\int_{X\times Y}c(x,y)d\pi+\int_{X}\varphi d(\mu-P^{X}_{\#}\pi)+\int_{Y}\psi d(\nu-P^{Y}_{\#}\pi)\right)\label{eq:M} \end{equation}

我们在\((\varphi,\psi)\in C^{0}_{b}(X)\times C^{0}_{b}(Y)\)取方程右边的上界，如下：

\begin{equation} \sup_{\varphi\in C^{0}_{b}(X)}\int_{X}\varphi d(\mu-P^{X}_{\#}\pi)=\left\{\begin{array}{ll}+\infty & {\rm if}~\mu\neq P^{X}_{\#}\pi\\0 & {\rm else.} \end{array}\right. \end{equation}

因此，在\(\pi\)上的下界就在\(P^{X}_{\# }\pi=\mu\)的时候取到，同理，\(P^{Y}_{ \# }\pi=\nu\)，重写公式(\(\ref{eq:M}\))有 \begin{equation} M=\inf_{\pi\in\mathcal{M}_{+}(X\times Y)}\sup_{(\varphi,\psi)}\left(\int_{X\times Y}c(x,y)-\varphi(x)-\psi(y)d\pi+\int_{X}\varphi d\mu + \int_{Y}\psi d\nu\right). \end{equation} 根据自变量的影响范围整理上面公式得到： \begin{equation} M=\sup_{(\varphi,\psi)}\left(\int_{X}\varphi d\mu+\int_{Y}\psi d\nu+\inf_{\pi\in\mathcal{M}_{+}(X\times Y)}\int_{X\times Y}c(x,y)-\varphi(x)-\psi(y)d\pi\right). \end{equation} 假如存在\((x_{0},y_{0})\in X\times Y\)和\(\epsilon>0\)使得\(\varphi(x_{0})+\psi(y_{0})-c(x_{0},y_{0})=\epsilon>0\)，然后通过令\(\pi_{\lambda}=\lambda\delta_{(x_{0}, y_{0})}\)，对于任意的\(\lambda>0\)我们有： \begin{equation} \inf_{\pi\in\mathcal{M}_{+}(X\times Y)}\int_{X\times Y}c(x,y)-\varphi(x)-\psi(y)d\pi\leq -\lambda\epsilon \rightarrow -\infty\quad{\rm as}\quad\lambda\rightarrow\infty. \end{equation}

因此，\(M\)的下界可以限制为当\(\varphi(x)+\psi(y)\leq c(x,y)\)时，所有\((x,y)\in X\times Y\)，也就是\((\varphi,\psi)\in \Phi_{c}\)（这种启发式的争论其实是用\((\varphi,\psi)\in C^{0}_b(X)\times C^{0}_{b}(Y)\)而不是\(L^{1}(\mu)\times L^{1}(\nu)\)这和限制\(\varphi(x)+\psi(y)\leq c(x,y)\)处处存在有些不同，是几乎处处存在的，不过这些更深入的细节这里暂时不做讨论），当\((\varphi,\psi)\in\Phi_{c}\)有： \begin{equation} \inf_{\pi\in\mathcal{M}_{+}(X\times Y)}\int_{X\times Y}c(x,y)-\varphi(x)-\psi(y)d\pi=0 \end{equation} 在\(\pi \equiv 0\)成立（例如），因此： \begin{equation} \inf_{\pi\in\prod(\mu, \nu)}\mathbb{K}(\pi)=\sup_{(\varphi,\psi)\in \Phi_{c}}\int_{X}\varphi(x)d\mu(x)+\int_{Y}\psi(y)d\nu(y) \end{equation} 这就是Kantorovich对偶的形式了，关于它的详细证明还需要很多篇幅。可以参考Introduction to Optimal Transport。

Sinkhorn 距离

随着最优传输所使用的维度升高，最优传输的求解复杂度很快就会变得不可接受。所以Marco Cuturi,2013²等提出从熵最大化的角度来看待传输问题。在原始的最优传输形式中加入传输方案熵正则化项来平滑经典的最优传输问题，这种新形式下的优化就可以通过Sinkhorn’s matrix scaling算法来解决。这种修改后的计算方式可以大大加快原始的最优传输优化形式的求解。

对于任意两个概率向量\(\mu,\nu\in\Sigma_{d}:=\{x\in \mathbb{R}^{d}_{+}:x^{T}\mathbf{1}_{d}=1\}\)，用\(U(\mu,\nu)\)表示\(\mu\)和\(\nu\)的传输可行空间： \begin{equation} U(\mu,\nu):={P\in\mathbb{R}^{d\times d}_{+}|P\mathbf{1}_{d}=\nu,P^{T}\mathbf{1}_{d}=\mu} \end{equation} 其中任意矩阵\(P\in U(\mu,\nu)\)其中\(p(X=i,Y=j)=p_{ij}\)，然后定义熵\(h(P)\)： \begin{equation} h(P)=-\sum^{d}_{i,j=1}p_{ij}\log p_{ij} \end{equation} 给定一个\(d\times d\)的代价矩阵\(M\)，那么从\(\mu\)传输到\(\nu\)的传输代价就可以写成： \begin{equation} d_{M}(\mu,\nu):=\min_{P\in U(\mu,\nu)}\langle P, M\rangle. \end{equation} 当矩阵\(M\)本身是一个度量矩阵时，即当\(M\)属于距离矩阵的锥时： \begin{equation} \mathcal{M}={M\in\mathbb{R}^{d\times d}_{+}:\forall i,j\leq d,m_{ij}=0\Leftrightarrow i=j,\forall i,j,k\leq d,m_{ij}\leq m_{ik}+m_{kj}} \end{equation} 联合分布中的熵限制(Cover and Thomas,1991,section 2): \begin{equation} \forall \mu,\nu\in\Sigma_{d},\forall P\in U(\mu,\nu),h(P)\leq h(\mu)+h(\nu), \end{equation} 当\(\mu\)和\(\nu\)相互独立的时候有\(h(\mu\nu^{T})=h(\mu)+h(\nu)\)，利用这个熵的凸性质，可以有： \begin{equation} U_{\alpha}(\mu,\nu):={P\in U(\mu, \nu)|KL(P||\mu\nu^{T})\leq \alpha}={P\in U(\mu, \nu)|h(P)\geq h(\mu)+h(\nu)-\alpha} \end{equation} 因此，就可以把对\(\mu\nu^{T}\)的KL散度小于某个阈值的\(P\)的集合解释为一系列在\(U(\mu,\nu)\)中的联合分布\(P\)，它对\(h(\mu)\)和\(h(\nu)\)有足够的熵，或者足够小的互信息。

所以定义Sinkhorn Distance为： \begin{equation} d_{M,\alpha}(\mu,\nu):=\min_{P\in U_{\alpha}(\mu,\nu)}\langle P, M\rangle. \end{equation}

之所以考虑在最优传输中使用熵的限制是因为，经典的线性规划的结果都是在可行域的顶点上取到。这样的一个\(d\times d\)维度的顶点通常最多只有\(2d-1\)个非零的元素。从概率的角度看这个顶点则是一个准确定性联合分布，因为一旦某一行有个元素\(p_{ij}>0\)，这一行的其他元素\(p_{ij'}\)其中\(j'\neq j\)就很少是非零的了。

另外再证明了三角不等式： \begin{equation} d_{M,\alpha}(x,z)=\min_{P\in U_{\alpha}(x,z)}\langle P,M\rangle \leq\langle S, M\rangle\leq d_{M,\alpha}(x,y)+d_{M,\alpha}(y,z) \end{equation} 可以大致确认通过一些优化手段是可以找到最优解的，然后考虑有熵限制条件的优化问题： \begin{equation} {\rm For}~\lambda>0,d^{\lambda}_{M}(\mu,\nu):=\langle P^{\lambda},M\rangle,~{\rm where}~P^{\lambda}={\rm argmin}_{P\in U(\mu, \nu)}\langle P,M\rangle-\frac{1}{\lambda}h(P). \end{equation} 基于对偶理论有任意的\(\alpha\)对应于一个\(\lambda\in[0, +\infty]\)使得\(d_{M,\alpha}(\mu,\nu)=d^{\lambda}_{M}(\mu, \nu)\)，这个\(d^{\lambda}_{M}\)就叫做dual-Sinkhorn divergence，它可以被很方便地计算得到。

从上图也可以看到传输方案\(P^{\lambda}\)的熵随着\(\lambda\)的增大而单调递增，我们可以通过不断增大\(\lambda\)直到\(h(P^{\lambda})\)到达\(h(\mu)+h(\nu)-\alpha\)。

通过Matrix Scaling Algorithm来对\(d^{\lambda}_{M}\)进行求解，对于任意\(\lambda>0\)有唯一解\(P^{\lambda}={\rm diag}(\mu)K{\rm diag}(\nu)\)，其中\(K:=e^{-\lambda M}\)。

利用拉格朗日乘子法和对偶变量\(\alpha,\beta\in\mathbb{R}^{d}\)代入\(U(\mu,\nu)\)中的限制条件： \begin{equation} \mathcal{L}(P,\alpha,\beta)=\sum_{ij}\frac{1}{\lambda}p_{ij}\log p_{ij}+p_{ij}m_{ij}+\alpha^{T}(P\mathbf{1}_{d}-\mu)+\beta^{T}(P\mathbf{1}_{d}-\nu). \end{equation} 取\(\frac{\partial \mathcal{L}}{\partial p_{ij}}=0\)可以推出\(p_{ij}=e^{-1/2-\lambda\alpha_{i}}e^{-\lambda m_{ij}}e^{-1/2-\lambda\beta_{i}}\)，\(P^{\lambda}\)因此就必定是对应的矩阵，可以通过Sinkhorn’s固定点迭代\((r,c)\leftarrow(\mu./Kr,\nu./K'c)\)得到。

补充资料

符号说明

• \(C^{0}_{b}(Z)\) 是定义在\(Z\)上的全体连续有界函数
• \(\mathcal{M}_{+}(Z)\) 是\(Z\)上正的拉东测度的集合
• \(\mathcal{P}(Z)\)是在\(Z\)上的概率测度的集合，也就是\(\mathcal{M}_{+}(Z)\)有单位质量的子集

测度

测度用于表示我们对于大小的直观概念，比如长度、面积、体积和质量等，有了这种度量我们才能将严格地讨论它们，并且将它们扩展一些直观上无法理解其大小的领域，比如函数空间。

一个测度就是一个函数，例如 \(\mu\) 从一个 \(\sigma\)-代数到一个非负的实数值，0 就表示一个空集，而当一个集合由很多互斥的子集 \(\{X_{i}\}\) 组成时，我们则有： \begin{equation} \mu(\cup X_{i})=\sum\mu(X_{i}) \end{equation} 直观的理解就是，如果两个集合它们之间没有任何交集，则把它们合在一起获得的新的并集大小就是它们各自的大小之和。

概率测度

如果全集的测度值被定义为 1，那这个测度就可以称为一个概率测度。在理论测量概率中，我们定义一个 \(\sigma\)-代数集，是一个包括了所有可能性的集合。我们拿出其中的一个子集来举例，扔出去的一个骰子可能是 1 也可能不是 1（某个子集），可能是偶数也可能是其他（另一个子集）。子集的度量称为定义它的事件的概率。

• 概率空间：一个概率空间是一个 \(X\) 集合的三倍，一个超过它的 \(\sigma\)-代数，\(\mathcal{X}\)，和一个概率测度 \(\mu\)
• 可测空间：一个可测空间是一组集合 \(X\) 连同其子集的 \(\sigma\)-代数的对
• 测度空间：一个测度空间是一个 \(X\) 集合的三倍，一个其子集的 \(\sigma\)-代数，和一个测度 \(\mu\)

推进测度

假设有一个映射满足 \(T:\mathcal{X}\rightarrow \mathcal{Y}\)，那么\(\mu\) 通过 \(T\) 映射的推进测度（pushforward measure）满足 \begin{equation} T_{\# }\mu(\mathcal{Y})=\mu(T^{-1}(\mathcal{X})) \end{equation} 其中，因为 \(\mu\) 是测度，\(\mathcal{X},\mathcal{Y}\) 是数据集，所以二者计算的符号不同用以区别。这里的 \(T^{-1}(\mathcal{X})\) 表示集合 \(A\) 的原像，而不是将 \(T\) 的逆函数应用到 \(A\) 上。

概率形式的边缘分布约束 \(\text{proj}_{ \# }^{x}\gamma = \mu\)，也就相当于上面提到的 \(\sum_{k} \Pi_{n k}=m_{n}\)。

传输方案

假如 \(\gamma\) 有一个密度函数 \(p(x,y)\) 它的意思就是指把 \(x\) 上的土运到对应的 \(y\) 上形成一个分布，而不是某个单点。假如最优的传输方案如下图所示，右边就是 Monge problem 的解法，而 Kantorovich 的形式则约束更为宽松。

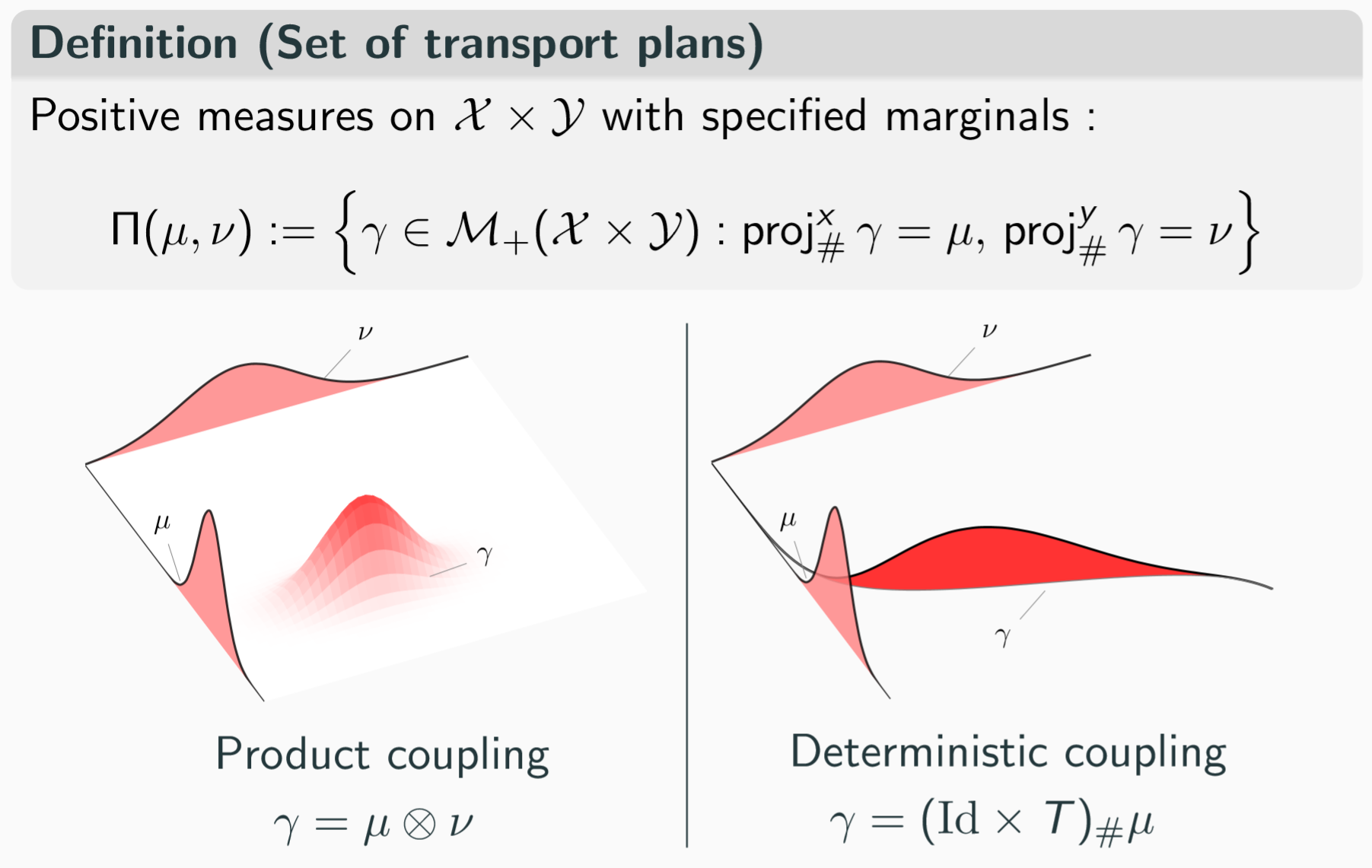
两个分布的联合分布如上图所示³，同样的离散表示形式可以表示成下面的形式：

更一般的传输方案优化目标可以写成下面的形式： \begin{equation} C(\mu, \upsilon):=\min_{\gamma\in \Pi(\mu, \upsilon)}\int_{\mathcal{X}\times\mathcal{Y}}c(x,y)d\gamma(x, y) \end{equation}

最优传输散度

在很多应用场景中，我们更加关心两个分布之间的距离而不是要把一个分布转化到另一个分布的传输方案。所以用最优传输的代价来表示这两个分布之间的差异下界。

假如输入是两个分布 \(\mu\) 和 \(\upsilon\)，我们有两个分布之间的最优传输代价为： \begin{equation} \text{OT}_{c}[\mu, \upsilon] = \int_{\mathcal{X}\times\mathcal{Y}}c(x,y)d\gamma(x, y), \end{equation} 其中的代价函数 \(c(x,y)\) 可以有很多种选择：

• \[\| x-y\| _{1}\]
• \[\| x-y\| _{2}\]
• \[\| x-y\| _{2}^{2}\]

如果将 \(\| x-y\| _{2}^{2}\) 代入则有 Wasserstein 距离为：

\begin{equation} W_{2}[\mu,\upsilon]=\inf_{\gamma}\int |x-y|_{2}^{2}d\gamma(x,y) \end{equation}

对于两个分布（概率测度）\(\mu\in\mathcal{P}(\mathcal{X}),\upsilon\in\mathcal{P}(\mathcal{Y})\)，他们之间的最优传输代价总和即为 \(C(\mu,\upsilon)\)，但是原始问题不太好求解，因为有时候可能根本没有解法，所以采取对偶问题来进行求解：

\[\begin{aligned} \min_{\gamma\in \Pi(\mu, \upsilon)} & \int_{\mathcal{X}\times\mathcal{Y}}c(x,y)d\gamma(x, y)\quad & (\text{Primal}) \\\\ \max_{\phi\in L^{1}(\mu)\\\\\psi \in L^{1}(\upsilon)} & \{\int_{\mathcal{X}}\phi(x)d\mu(x)+\int_{\mathcal{Y}}\psi(y)d\upsilon(y):\phi(x)+\psi(y) \leq c(x,y)\}\quad & (Dual) \end{aligned}\]

其中既要满足边缘分布的约束，也要保证两个相同分布之间的散度为零。\(\phi,\psi\) 分别表示两个分布的移动策略，这个策略能够使它们相互靠近。

当最优条件满足的时候下面成立：

• 对于 \(\gamma\) 而言，\(\phi(x)+\psi(y)=c(x,y)\) 几乎在每一个 \((x,y)\) 位置上都成立
• \(\gamma\) 集中在一个 c-周期性单调集上。

最优传输是线性规划的问题的一个特例，因为要优化的函数和约束都是传输图的线性函数。线性规划的一个基本结果就是所有的线性问题都存在对偶问题。

参考

关于对偶问题在离散化最优传输及线性规划中的解释可以进一步看从Wasserstein距离、对偶理论到WGAN⁴

---